9. Derivate in un punto e funzione derivata
La lezione 9 ha riguardato:
- Calcolo della derivata di una funzione in un punto
- Calcolo della funzione derivata di una funzione
8. Limiti e cenno di derivata
La lezione 8 ha riguardato:
- Esempi di limiti
- Teoremi sulle successioni monotòne
Esempi di limiti
- f non è continua in zero
- 0 è asintoto verticale
- f(x) non ha né minimo né massimo e non è limitato perché non è continuo in zero (ha asintoto ma non limite)
- i teoremi dei valori intermedi e di Weierstraß necessitano di una funzione continua, quindi non sono applicabili
Appunti di calcolo / tu sopra io sotto, ovvero le equazioni razionali
Regola generale: se il divisore e il dividendo sono uguali, il risultato è un valore costante 1 con dominio ℝ\{0} (per tutta la trattazione si esclude implicitamente o esplicitamente quandi il divisore è zero)
Se sono diversi, appare un'iperbole (magari "distorta"), nei quadranti 1, 3 se la frazione ha segno positivo, nei quadranti 2, 4 se ha segno negativo. Keep reading →
Appunti di calcolo / riflessioni (piccole piccole) sulle equazioni di terzo grado
Leggevo su qualche libro che per risolvere tutte le soluzioni delle equazioni di III grado è necessario conoscere (bene) i numeri complessi ℂ, ma dopo l'ultima lezione sulle derivate improvvisamente sono diventato "esperto" di queste equazioni.
In particolare, sono rimasto molto colpito da come è possibile far corrispondere una funzione di III grado con una di II che ne rappresenta la funzione derivata. Keep reading →
Appunti di calcolo / logaritmi
Il logaritmo di un numero x in base a è il numero per cui è necessario elevare a per ottenere x:
Esempio:
Appunti di calcolo / Funzioni razionali
I prof tendono a essere precisi e a dare definizioni esatte, soprattutto quelli di matematica.
Però questi appunti si possono chiamare, in confidenza, anche "funzioni con la x sotto" o "funzioni con l'incognita al divisore".
La più famosa è 1/x:
Appunti di calcolo / funzioni di secondo grado
Dopo aver scritto un piccolo riepilogo sulle parabole e la corrispondenza tra grafico e termini dell'equazione, facciamo qualche considerazione sul significato di vertice.
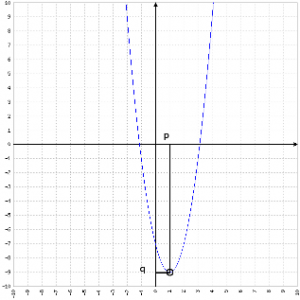
Definiamo il vertice della parabola V=(p,q) e definiamo a, b, c, nella maniera "classica" i fattori che moltiplicano rispettivamente x2, x1 (cioè x), x0 (quindi c è costante): in pratica l'equazione della parabola è ax2+bx+c.
7. Limiti e asintoti
La lezione 7 ha riguardato:
- Esempi di limiti
- Asintoti
- Teoremi sulle funzioni continue
Esempi di limiti
Dimostrazione che (1+t)n≥1+nt (disuguaglianza di Bernoulli)
Con t∈ℝ e t>-1, ∀ n∈ℕ
Dim. per induzione (1) base: per n=1, (1+t)1 = 1+t ≥ 1+(1·t) = 1+t (2) passo induttivo: Supponiamo per n>1
Sviluppiamo calcolando il passo n+1, moltiplicando entrambi i membri per 1+t
Appunti di calcolo / trigonometria
Per la trattazione di questo tema parto dal sapere già come sono rappresentati il seno e il coseno in una circonferenza goniometrica, perché, sì, ho fatto il classico, però fino a qui ci sono.
Il bello di seno e coseno è che elevando al quadrato i due valori si ottiene sempre la retta che - nel contesto della circonferenza goniometrica - vale sempre 1.
Quindi: sin(x)2+cos(x)2=12, che è sempre 1.
Appunti di calcolo / rette
Questa è l'equazione y = x:
Qualche riflessione:
- questa è la retta attraverso cui si riflette una funzione: f(x) e f-1(x) sono lo stesso grafico specchiato su questa retta