Il logaritmo di un numero x in base a è il numero per cui è necessario elevare a per ottenere x:
Esempio:
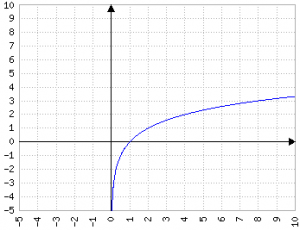
Table of Contents
Alcune proprietà evidenti
Siccome qualunque numero elevato alla zero (tranne zero) da uno, qualunque logaritmo sensato (con base positiva) passa per il punto (1,0).
Per ogni valore compreso tra 0 e 1 (esclusi) il valore del logaritmo è negativo e decresce in maniera esponenziale (letteralmente) con il diminuire di x, per es. per 1/2:
per 1/4:
Per ogni valore superiore a 1 il valore del logaritmo è positivo e tende a +∞ (molto mooolto lentamente, ma lo fa)
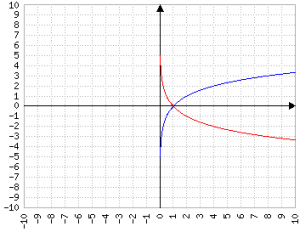
Se la base è compresa tra 0 e 1 il grafico si "ribalta":
Altre proprietà meno evidenti
Alcune proprietà interessanti dei logaritmi sono somma, sottrazione, prodotto e divisione di logaritmi:
somma: log(a·b) = log(a)+log(b)
sottrazione: log(a/b) = log(a)-log(b)
prodotto: log(ab) = b·log(a)
divisione: log(√a) = 1/2·log(a)
[S]Cambio di base
Una delle proprietà più usate e importanti dei logaritmi è il cambio di base: se dobbiamo fare operazioni su logaritmi con basi diverse, o anche solo con basi "scomode" da calcolare, possiamo trasformare il logaritmo in questo modo:
Ricordarla è semplice: il termine scritto più "in alto" va "in alto" nella frazione, il termine più "in basso" va "in basso". In termini più formali, l'argomento va al dividendo, la base al divisore (più formale, ma più difficile da ricordare).
Ora, poiché logaa = 1 (per ottenere a da a devo elevare a alla 1, ∀ a≠0):
Fuori l’esponente!
Un'altra proprietà importante è la possibilità di portare fuori l'esponente dell'argomento...
...e della base...
...e - ovviamente - di entrambi:
e
Probabilmente dovrei dedicare a e una scheda a parte, ma per il momento butto lì qualche riflessione preliminare.
e≃2,71
e∈ℝ\ℚ, quindi non è rappresentabile direttamente come numero o frazione, ma solo come approssimazione o con una funzione che lo rappresenti.
Tale funzione è la serie infinita (si definisce 0! = 1, cioè zero fattoriale uguale uno):
Può essere definita anche come limite: