Triangolo di Tartaglia
Il Triangolo di Tartaglia

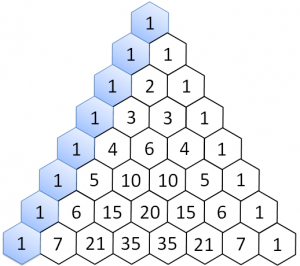
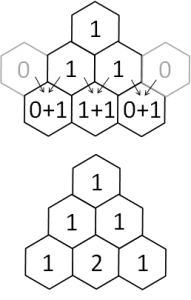
Il triangolo di Tartaglia è una "tabella" di numeri che si costruisce partendo da 1 (per il triangolo classico) e aggiungendo livelli sotto, ciascuno di un elemento in più di quello sopra.
Gli elementi del livello successivo sono la somma degli elementi immediatamente sopra.
Il coefficiente binomiale
La corrispondenza tra le righe del triangolo e il numero di riga è utile in molti casi:
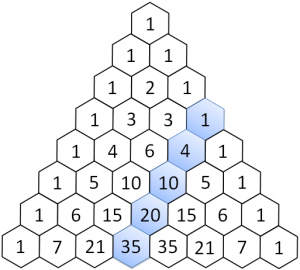
0 ⇒ 1
1 ⇒ 1, 1
2 ⇒ 1, 2, 1
3 ⇒ 1, 3, 3, 1
4 ⇒ 1, 4, 6, 4, 1
5 ⇒ 1, 5, 10, 10, 5, 1
Per esempio, l'n-esima riga del triangolo dice qual è il coefficiente nello sviluppo di un polinomio.
Nota: si assume che la prima riga, contenente solo 1, sia la "riga zero".
Un paio di esempi possono essere più chiari.
Voglio risolvere (a+b)2. Corrisponde a (a+b)(a+b), quindi a*a + a*b + b*a + b*b, e quindi a2+2ab+b2.
Voglio risolvere (a+b)3. Corrisponde a (a+b)(a+b)(a+b). Ora sappiamo che (a+b)(a+b) = a2+2ab+b2, quindi possiamo scrivere (a2+2ab+b2)(a+b). Otteniamo a2*a+a2*b+2ab*a+2ab*b+b2*a+b2*b, che raggruppando i termini uguali corrisponde a a3+3a2b+3ab2+b3.
Se volessi risolvere (a+b)4 sarei costretto a numerosi (e noiosi) passaggi, per ottenere alla fine a4+4a3b+6a2b2+4ab3+b4
Con un po' di spirito di osservazione, notiamo che in tutti i polinomi abbiamo un grado che sale e uno che scende (nel nostro esempio, a sale e b scende): per esempio in un polinomio di grado 4, a scende da 4 a zero: 1a4b0+4a3b1+6a2b2+4a1b3+1a0b4 mentre il grado di b sale 1a4b0+4a3b1+6a2b2+4a1b3+1a0b4
Per quanto riguarda invece i coefficienti, notiamo che sono dati esattamente dalla riga del triangolo di Tartaglia corrispondente al grado del polinomio: 1a4b0+4a3b1+6a2b2+4a1b3+1a0b4
Se volessi risolvere quindi (a+b)5 mi basterebbe:
inserire a con esponente da 5 a 0 a:
| a5 | + | a4 | + | a3 | + | a2 | + | a1 | + | a0 |
inserire b con esponente da 0 a 5:
| a5 | b0 | + | a4 | b1 | + | a3 | b2 | + | a2 | b3 | + | a1 | b4 | + | a0 | b5 |
inserire il coefficiente binomiale della sesta riga, corrispondente al polinomio di grado 5:
| 1 | a5 | b0 | + | 5 | a4 | b1 | + | 10 | a3 | b2 | + | 10 | a2 | b3 | + | 5 | a1 | b4 | + | 1 | a0 | b5 |
Poi - se voglio - riscrivo lo sviluppo togliendo gli esponenti a zero e a uno, per essere un po' più elegante:
a5+5a4b+10a3b2+10a2b3+5ab4+b5
Notazioni matematiche
Il coefficiente binomiale si indica con
in cui n è il numero della riga e k è il numero dell'elemento.
Convenzionalmente k ≤ n; se invece k > n si assume che il valore sia 1 (valore costante).
Il calcolo del coefficiente binomiale è dato da
Coefficiente e statistica
Il lancio di una moneta (non truccata) può dare come esito uno tra due risultati equivalenti.
Se lancio più volte la moneta ottengo un albero di possibilità (non probabilità!), che corrisponde, per quattro lanci, al seguente (T = Testa, C = Croce):
| 0 | (non ho ancora lanciato) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | T | C | ||||||||||||||
| 2 | T | C | T | C | ||||||||||||
| 3 | T | C | T | C | T | C | T | C | ||||||||
| 4 | T | C | T | C | T | C | T | C | T | C | T | C | T | C | T | C |
Al termine dei quattro lanci ho sicuramente seguito uno e uno solo dei sedici percorsi possibili.
Noto che i percorsi sono sedici perché non ho ancora lanciato mai la moneta: infatti se al primo lancio ottenessi croce, le probabilità che possa seguire un percorso "a sinistra" diventano zero.
Le probabilità che ottenga sempre testa sono 1/16, così come le probabilità che ottenga sempre croce (questa è facile), ma quante probabilità ci sono che ottenga esattamente due volte testa? Sono le stesse che ottenga esattamente croce (anche questa è facile), ma contiamole:
| 0 | (non ho ancora lanciato) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | T | C | ||||||||||||||
| 2 | T | C | T | C | ||||||||||||
| 3 | T | C | T | C | T | C | T | C | ||||||||
| 4 | T | C | T | C | T | C | T | C | T | C | T | C | T | C | T | C |
e contiamo con altri colori le volte che ottengo tre volte testa o tre volte croce:
| 0 | (non ho ancora lanciato) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | T | C | ||||||||||||||
| 2 | T | C | T | C | ||||||||||||
| 3 | T | C | T | C | T | C | T | C | ||||||||
| 4 | T | C | T | C | T | C | T | C | T | C | T | C | T | C | T | C |
Ci sono:
- 1/16 probabilità di ottenere quattro teste
- 4/16 = 1/4 di ottenere tre teste e una croce
- 6/16 = 3/8 di ottenere due teste e due croci
- 4/16 = 1/4 di ottenere tre croci e una testa
- 1/16 probabilità di ottenere quattro croci
Controprova: sommo tutte le probabilità e ottengo 16/16.
Anche in questo caso, il triangolo di Tartaglia riporta esattamente le probabilità di testa o croce leggendo l'n-esima riga come l'n-esimo lancio. Notiamo che la prima riga corrisponde a non aver ancora lanciato, e per convenzione è 1.
Caratteristiche del TdT
Somma delle righe
Le possibilità di lanci di moneta sono esponenti di due: al primo lancio ho 21 possibilità (T, C), al secondo lancio ne ho 22 (TT, TC, CT, CC), al terzo ne ho 23 (TTT, TTC, TCT, TCC, CTT, CCT, CTC, CCC), al quarto ne ho 24 e così via.
Per questo la somma di ciascuna riga del TdT è un esponente di due:
riga 0: 1 = 20
riga 1: 1+1 = 21
riga 2: 1+2+1 = 22
riga 3: 1+3+3+1 = 23
e così via
Simmetria
Il TdT è simmetrico lungo l'asse centrale. Questo può essere visto come una conseguenza del fatto che testa e croce, dal punto di vista della probabilità, sono equivalenti, così come la scelta di a e b nel binomio.
Questo significa che l'elemento k della riga n e l'elemento n-k+2 della riga n sono sempre uguali.
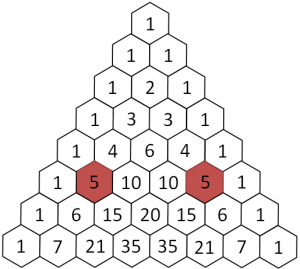
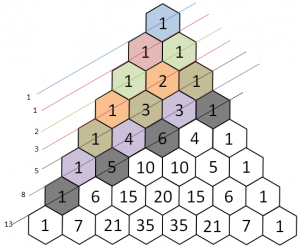
Diagonale zero
La prima diagonale, che chiameremo "diagonale zero" è una serie di 1.
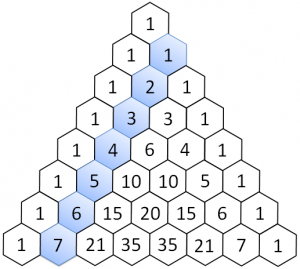
Prima diagonale
La prima diagonale è un progressivo, che rappresenta il numero di riga partendo da zero.
Seconda diagonale
La seconda diagonale si ottiene aggiungendo la differenza tra l'elemento e quello precedente più uno.
Il primo elemento è 1. Il secondo elemento è dato dalla differenza tra il precedente (0) e il corrente (1) più uno = 3.
Il terzo è 3+(3-1)+1 = 6, il quarto 6+(6-3)+1 e così via.
In modo ricorsivo, si ha che
f(n) = {1 se n = 1; f(n-1)+[f(n-1)-f(n-2)]+1 altrimenti}
La definizione ricorsiva è poco agevole: per fortuna, con un po' di intuizioni "geometriche" è possibile trovare una formula più facile.
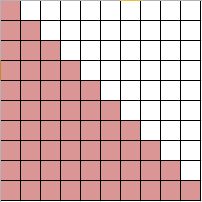
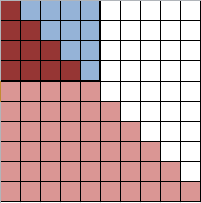
Questa immagine rappresenta una serie in cui nella prima riga c'è un elemento, nella seconda due e così via. Ebbene, la somma di tutti i quadrati fino a una certa riga corrisponde esattamente al numero resitituito dalla terza diagonale di Tartaglia.
Per come sono costruiti questi numeri, vengono detti numeri "triangolari".
Facciamo un esempio per n=4:
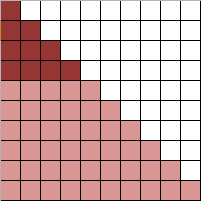
Se aggiungiamo ai "quadratini" che rappresentano il numero, altrettanti "quadratini", otteniamo un rettangolo di dimensione n*(n+1)
Con qualche facile trasformazione, otteniamo che la formula per ottenere il numero corrispondente all'elemento n-esimo della diagonale è
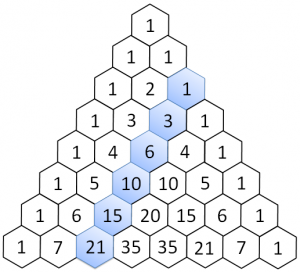
Terza diagonale
La differenza tra l'elemento n-esimo e n+1-esimo della terza diagonale corrisponde al numero precedente della seconda: 4-1 = 3, 10-4 = 6, 20-10 = 10 eccetera.
La terza è l'ultima diagonale trattata, perché dalla quarta in poi il principio è sempre uguale. A dirla tutta, anche per le diagonali precedenti valeva lo stesso, ma era più semplice trattare il problema specifico che quello generico.
La formula "secca" per ottenere la serie della quarta diagonale è
Il fatto che n sia moltiplicato per sé stesso tre volte fa intuire una corrispondenza geometrica tra la serie e una figura tridimensionale.
Infatti, in un tetraedro composto da "palline", il numero di palline totali a un certo livello corrisponde al numero della terza diagonale:
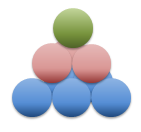
Generalizzazione
La formula generalizzata per il calcolo dei numeri della k-esima diagonale è quindi:
Per farla ancora più semplice, in excel è
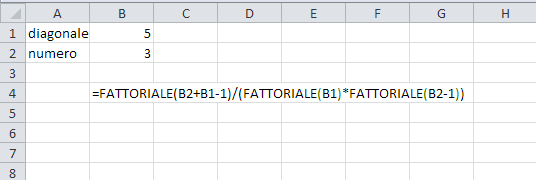
Ovviamente la formula funziona con qualunque riga, anche con quelle già discusse.
Questa formula è utile in matematica combinatoria e in statistica perché è quella che si usa nelle combinazioni con ripetizioni (quelle che rispondono alla domanda "Ho 12 penne e 5 cassetti. In quanti modi posso distribuire le penne nei cassetti?")
Fibonacci
Le "semi-diagonali" del triangolo, se sommate, danno i numeri di fibonacci.
Un numero di Fibonacci è dato dalla somma dei due numeri precedenti, tranne i primi due che sono sempre 1 e 1: la serie è quindi 1, 1, 2, 3, 5, 8, 13, 21, 34...
Undici
11 è un numero che contiene le cifre della riga 1
112 contiene le cifre della riga 2
113 contiene le cifre della riga 3
114 contiene le cifre della riga 4
115 NON contiene le cifre della riga 5, perché una delle cifre della riga 5 è un 10, e nel sistema decimale (l'unico con cui "funziona" questo gioco) ha due cifre.