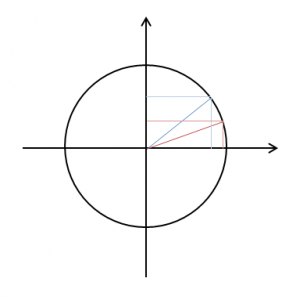
Per la trattazione di questo tema parto dal sapere già come sono rappresentati il seno e il coseno in una circonferenza goniometrica, perché, sì, ho fatto il classico, però fino a qui ci sono.
Il bello di seno e coseno è che elevando al quadrato i due valori si ottiene sempre la retta che - nel contesto della circonferenza goniometrica - vale sempre 1.
Quindi: sin(x)2+cos(x)2=12, che è sempre 1.
Seno e coseno sono quindi in una relazione strettissima, cioè sin(x)2 = 1-cos(x)2; sviluppando ancora: sin(x)=sqrt(1-cos(x)2) e lo stesso vale invertendo seno e coseno.
Parliamo ora di angoli: solitamente usiamo definire l'angolo come la 360esima parte di un cerchio, quindi 360° è l'angolo giro, 180° è l'angolo piano, 90° è l'angolo retto... (misura in gradi)
Nella trigonometria si usa invece misurare l'angolo in radianti, cioè si considera π angolo di 180° e si usano le frazioni di π per individuare gli altri angoli (misura in radianti).
Dunque l'angolo giro è 2π, l'angolo piano è π, l'angolo retto è π/2...
Il coseno è la funzione che identifica la proiezione sull'asse delle ascisse della retta di lunghezza 1:
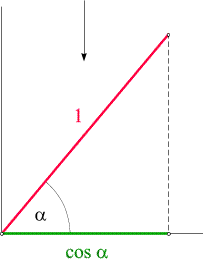
è evidente che quando x è positivo anche il coseno di x è positivo e viceversa.
Per il seno questa semplice relazione non vale, in quanto da 0 a π/2 e da 3/2π a 2π è zero o positivo, da π/2 a 3/2π è negativo (zero a π).
Somma degli angoli del seno/coseno
È evidente che finché si resta nel primo quadrante (cioè sin(x)+sin(y) ≥ 0 e cos(x)+cos(y) & ge; 0) la somma di angoli positivi porta ad aumentare il seno e a diminuire il coseno. Ma di quanto?
Nel primo disegno entrambi i triangoli sono costruiti sull'asse x, ma se ne mettiamo uno "sopra" l'altro, otteniamo qualcosa di simile a questo:
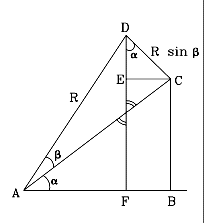
dove il triangolo blu del primo disegno è ABC e il triangolo rosso è ACD.
AD è il raggio del cerchio. Per ora possiamo considerare la circonferenza goniometrica, considerare AD = 1 e quindi lo escludiamo dal calcolo. Quando AD varrà qualcosa di diverso da 1 lo includiamo nella formula finale.
(1) BC è il seno dell'angolo α per la lunghezza del segmento AC, che (anche se dal disegno non si capisce molto) è il coseno di β. Quindi BC = sin(α)*cos(β)
Il triangolo ABC e i triangoli simili (tra cui AF e l'angolo segnato con una linea doppia) è composto da tre angoli, di cui uno è 90° e gli altri due, sommati tra loro, sono altri 90° (la somma degli angoli di un triangolo è sempre 180°), quindi sono α e 90-α.
Anche il triangolo DC e l'angolo segnato con una linea doppia è un triangolo rettangolo, nel vertice C, ed è il riflesso di un triangolo simile a AF e l'angolo segnato con una linea doppia, quindi l'angolo in D è α.
(2) Quindi possiamo calcolare DE e EC rispettivamente come il coseno e il seno di α moltiplicati per la lunghezza di DC, che è il seno di β.
BC è noto, perché è il seno di α per il coseno di β (1); DE è noto, perché è il coseno di α per seno di β (2), quindi DF è sin(α)*cos(β)+cos(α)*sin(β) = sin(α+β)
E con il coseno, come la mettiamo? Dobbiamo sottrarre EC a AB per ottenere AF: si può facilmente calcolare che AB = cos(α)*cos(β) (poiché AB è il coseno(α) costruito su AC che è a sua volta il coseno(β)) e EC = sin(α)*sin(β) (poiché EC è il seno(α) costruito su DC, che è a sua volta il seno(β)).
Quindi la formula è cos(α)*cos(β) - sin(α)*sin(β) = cos(α+β).
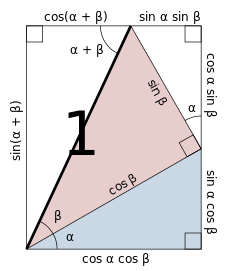
Qui un'altra immagine ancora più chiara (grazie Wikipedia):
Tangente e cotangente
La tangente è la funzione definita come rapporto tra seno e coseno (la cotangente è cos/sen)