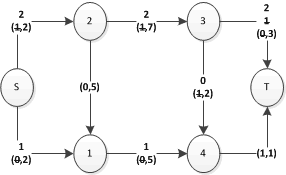
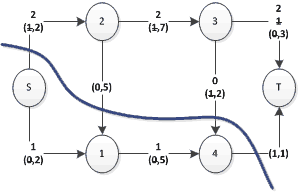
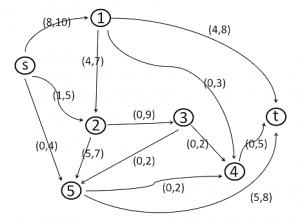
Ricerca Operativa - 19
OK, 19 non è un voto di cui esattamente vantarsi, e Obama non è più il Presidente degli USA e non elargisce medaglie, MA...
All'inizio del mio percorso di studi avevo preventivato che ci potevano essere due motivi per cui ero giustificato nel sospendere i miei studi per un annetto, e sono alla fine del più piacevole dei due.
In questo contesto, anche solo aver portato a casa un esame - l'unico che ho tentato - mi dà una soddisfazione immensa.
Quindi, Obama: recupera qualche medaglietta dal fondo del cassetto e...