Riflessioni sulla distribuzione di Poisson
La distribuzione di Poisson si propone di risolvere problemi simili a quelli della distribuzione binomiale, ma con le due caratteristiche che il campione sia molto grande e che la probabilità sia molto piccola.
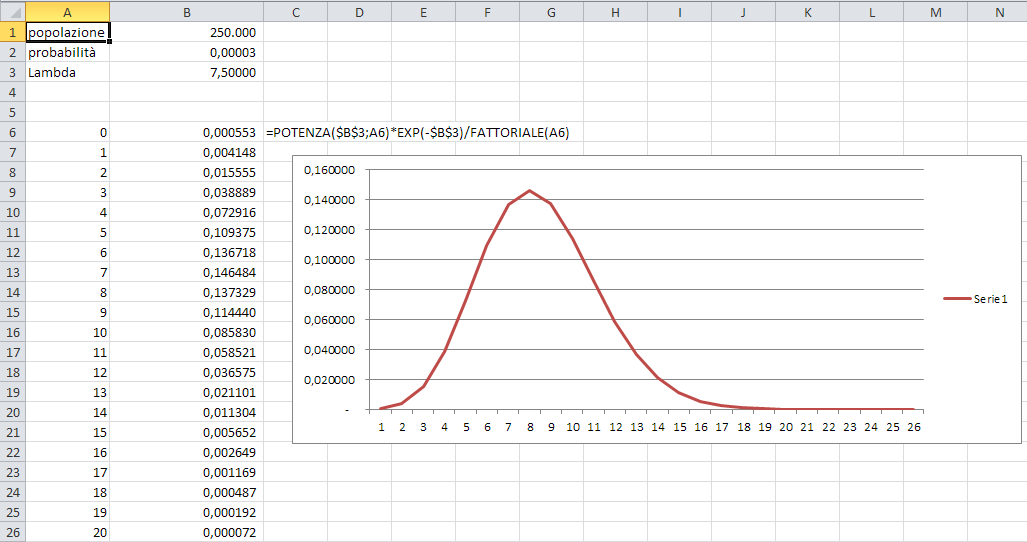
Per esempio, la probabilità che una persona abbia la sindrome di Krugen-Spassen è dello 0,003%, e la città di Mestre conta 250.000 persone. Quante probabilità ci sono che a Mestre ci sia qualcuno con la sindrome di Krugen-Spassen?
La risposta è 250.000 * 0,00003 = 7,5, cioè ci si può attendere che in tutta Mestre queste persone siano circa 7 o 8.
Applicando la "formulina" scopriamo quante probabilità ci sono che a Mestre ci siano esattamente tre persone con la sindrome:
abbiamo λ = 7,5, n = 3
quindi λn = 7,5^3 = 421,875, e^-λ = 0,000553
e P(X) = 0,03888
In definitiva, abbiamo circa il 4% di probabilità che ci siano esattamente tre persone in tutta Mestre.