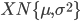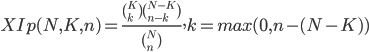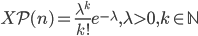Apici di R

Come caratteri di markdown, R usa gli apici "storti", che si ottengono con alt+96 oppure facendo copia e incolla da qui:

```{r}
```

Installazione pacchetti

A causa di un "bug" tra R e antivirus, il timeout di R per l'installazione di pacchetti nella cartella temporanea non è sufficiente.
Per questo, va eseguita la seguente istruzione:

trace(utils:::unpackPkgZip, quote(Sys.sleep(2)), at = which(grepl("Sys.sleep", body(utils:::unpackPkgZip), fixed = TRUE)))

Il testo completo del suggerimento.

I found that the problem indeed is the antivirus "real time file system protection". I do the following to fix the problem:
trace(utils:::unpackPkgZip, edit=TRUE)
I edit line 140 (line 142 in R 3.4.4):
Sys.sleep(0.5)
to:
Sys.sleep(2)
I seems like the antivirus stalls the creation of the package tmp dir. After changing it to 2 seconds the error is gone.
EDIT: to do this programmatically execute
trace(utils:::unpackPkgZip, quote(Sys.sleep(2)), at = which(grepl("Sys.sleep", body(utils:::unpackPkgZip), fixed = TRUE)))
(credits @DavidArenburg)

Librerie usate

Le librerie usate sono sei, e si possono installare e includere con le seguenti istruzioni:

install.packages(c("tigerstats", "MASS", "labstatR", "matrixcalc", "mvtnorm", "mnormt"))
library(tigerstats)
library(mnormt)
library(mvtnorm)
library(matrixcalc)
library(labstatR)
library(MASS)

Markov

In due compiti su tre ha dato come primo esercizio una catena di Markov. La so, quindi se la trovo devo puntare su quella per ottenere tutti e 10 i punti.

Controllare se c'è una catena di Markov e iniziare da lì.

Gli esercizi chiedono di:

1. costruire una matrice di probabilità
2. tramite l'operatore %*% si possono calcolare le matrici dei passi successivi
3. simulare una catena (ciclo while e vettore di risultati, uso di sample per probabilità specificate esplicitamente)
4. plot della catena
5. simulazione di n traiettorie per determinare media, varianza... (non serve il vettore). Il valore iniziale deve essere incluso dentro al for esterno

Esercizi obbligatori

Da questa sessione sono marcati come obbligatori alcuni esercizi. INIZIA DA QUELLI!!!

Normale

1. ATTENZIONE: nel testo può essere specificata la Scarto Quadratico Medio (SD, Standard Deviation) oppure la Varianza. Molta attenzione, perché ai comandi dnorm, pnorm, qnorm e rnorm va passato lo Scarto Quadratico Medio, mentre se il dato è la varianza ne va passata la radice quadrata:
   SD = SQM/SD oppure Sqrt(Var)
2. Se si chiede di reiterare la normale su più di un caso (es. presi 5 elementi con distribuzione normale...), la SD va divisa per la radice quadrata del numero di elementi.
3. Se si chiede, dati una media, un valore a campione e il suo percentile, di trovare la SD, si fa la differenza tra la media e il valore e si divide per qnorm(percentile). Se chiede la Varianza, elevare questo valore al quadrato

Variabili

Quando nel primo punto di un esercizio chiede di calcolare una variabile, probabilmente la userà nei punti successivi, quindi vale la pena di salvarla.

Attenzione che in qualche caso NON usa gli stessi parametri in tutto l'esercizio (es. cambia la SD).

Esercizi con distribuzioni diverse

Può dare esercizi in cui sono presenti due elementi con distribuzioni diverse, per esempio uno normale con probabilità 55% e uno poisson con probabilità 45%.

Chiede sempre:

1. Un esempio di distribuzione A
2. Un esempio di distribuzione B
3. Un esempio di distribuzione congiunta (es. A*0.55 + B*0.45)
4. Dato un evento con una certa probabilità (punto 3), determinare quale probabilità c'è che sia di A. In questo caso la probabilità P(A|cong) = A*0.55 / cong

La funzione plot prende come parametri:

1. un vettore di valori da posizionare nell'asse x
2. un vettore di valori da posizionare nel grafico, che dovrebbe essere di dimensione uguale al primo
3. un tipo:
   • p => points
   • l => lines
   • h => histogram
   • s => steps
   • altri meno interessanti
4. main = intestazione del grafico
5. sub = piè di pagina del grafico
6. xlab / ylab = etichette degli assi
7. asp = proporzione y/x