Le soluzioni di un'equazione con modulo sono, per
f:A→ℝ
|f(x)|=k
k < 0 ↠ impossibile
k = 0 ↠ f(x) = 0
k > 0 ↠ |f(x)|-k = 0
f:A→ℝ
f(x)=|x^2-5| = 1
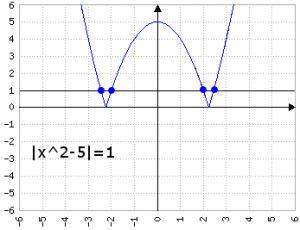
Il segno (positivo dentro il valore assoluto) indica che la parabola è rivolta verso l'alto; il Δ = +20 indica che esistono due soluzioni; però il valore assoluto fa raddoppiare ulteriormente le soluzioni, che diventano quattro perché il termine dopo l'uguale è ≠ 0.
La lezione 6 ha riguardato:
Vedere Lezione 5
Data la funzione
trovare il limite per x che tende a zero.
La lezione 5 ha riguardato:
Come già visto nella lezione precedente, è possibile esprimere ax con a, x∈ℝ come il limite per rk→x con k∈ℚ.
In pratica, "avviciniamo" arbitrariamente il valore di rk a x per approssimare a sufficienza il numero reale x.
La lezione 4 ha riguardato:
Data una funzione f:A→B posso costruire una f -1:f(A)→A dove f(A)⊆B tale che f-1∘f(a) = a ∀ a∈A e f∘f-1(b) = b ∀ b∈f(A).
Come regola, se non è esplicitamente richiesto che il dominio e il codominio di una funzione siano insiemi ℕ, ℤ o ℚ, il dominio su cui ci esercitiamo è quello dei numeri reali ℝ.
Le eccezioni più frequenti si riscontrano per prendere in considerazione tre casi particolari:
1) il dominio esclude lo zero, solitamente quando x sta al denominatore di una frazione.
f:ℝ→ℝ
f:x→1/x
non è valida, poiché con queste premesse x può essere = 0.
La lezione 3 ha riguardato:
Una qualunque f:ℕ→ℝ può essere scritta anche come
a1, a2, a3, ... an, con n∈ℕ
In una successione è possibile dimostrare un enunciato tramite il principio di induzione.
La lezione 2 ha riguardato:
La prima lezione ha riguardato: