5. Limiti / 1

La lezione 5 ha riguardato:

Definizione di limite
Definizione di punto di accumulazione
Proprietà dei limiti

Table of Contents

Definizione di limite

Come già visto nella lezione precedente, è possibile esprimere a^x con a, x∈ℝ come il limite per r_k→x con k∈ℚ.

In pratica, "avviciniamo" arbitrariamente il valore di r_k a x per approssimare a sufficienza il numero reale x.

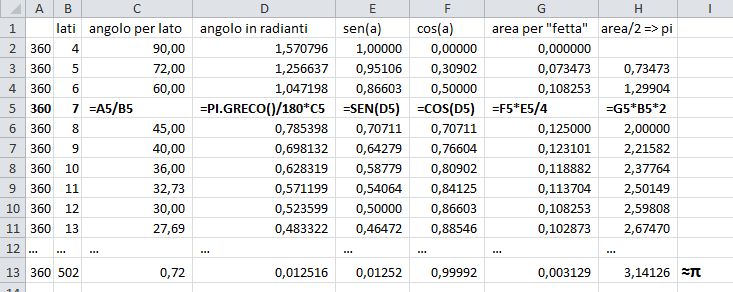
Alla stessa maniera possiamo approssimare l'area del cerchio come area del poligono inscritto (somma dei triangoli isosceli che hanno come lati uguali il raggio del cerchio e come terzo lato sen(α)²/cos(α). L'area del triangolo è ottenibile tramite sen(α)*cos(α)/4, moltiplicato per il numero di lati).

Fig.1: esempio di approssimazione fatto con Excel

Se definiamo A(n) come area del poligono inscritto,

$lim_{x \to +∞} A(x) = A(area del cerchio)$

Definizione di punto di accumulazione

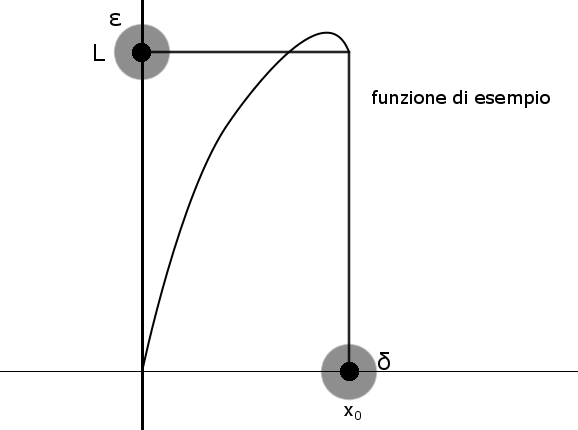
Dato un x₀ limite per una funzione f:A→ℝ,

$lim_{x \to x0} f(x)$

un punto di accumulazione x₀ è un punto non necessariamente appartenente al dominio A, ma in ogni intorno di x₀, per quanto piccolo, devono esserci solo punti di A (escluso x₀, eventualmente).

Definizione

Sia x₀ un punto di accumulazione per il dominio di f(x)=A
Diciamo che

$lim_{x \to x0} f(x) = L$

quando ∀ intorno I(L, ε) = {x∈A, ||x-L|<ε} ∃ un intorno I₁(x₀, δ) tale che ∀ x∈I₁(x₀, δ) f(x)∈I(L, ε)

Esempio di limite

Sia
f:ℝ→ℝ
f(x)=3x-1

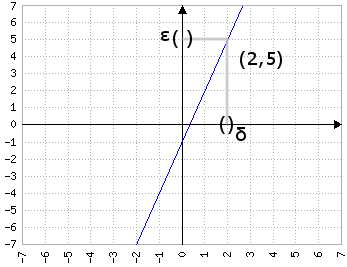
Vogliamo calcolare il limite per x che tende a 2 per f(x).

Applicando la definizione di limite, prendiamo un ε arbitrario; dobbiamo trovare un δ>0 tale che |3x-1-2|<ε (3x-1 è f(x), 2 è il limite) se 0<|x-2|<δ

δ dipende da f(x) e da ε

|3x-1-5|=|3x-6|=3|x-2|

Supponiamo che 3|x-2|<ε allora 0<|x-2|<ε/3 (ε/3 è il mio δ) allora 3|x-2|=|f(x)-L|<epsilon;

Proprietà dei limiti

Il limite può non esistere
Se esiste, il limite è unico
Può non esistere un limite, ma possono esistere un limite destro e un limite sinistro
La somma di due limiti è uguale al limite della somma delle funzioni
Se il limite di una funzione è compreso tra due limiti di funzioni con lo stesso limite, anche la prima ha lo stesso limite (teorema di compressione o dei due carabinieri)

Esempio di limite non esistente e di limiti destro e sinistro

Nel caso della funzione
f:ℝ→ℝ
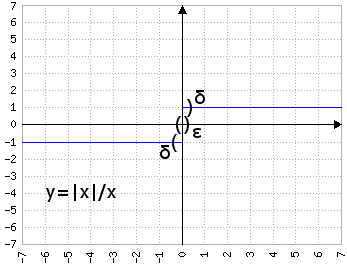
f(x)=|x|/x, x≠0

il punto di accumulazione 0 è esterno al dominio, mentre il limite per x→0 è ambiguo, perché l'intorno di destinazione δ è disgiunto.

Per questa funzione non esiste limite per x→0, ma è possibile comunque definire un limite destro (prende in considerazione solo la parte positiva dell'intorno) e un limite sinistro (solo quella negativa). In entrambi i casi il limite è zero, ma non si tratta del limite unico, ma di due limiti diversi.

Definizione di somma di limiti

Dati due limiti:

$lim_{x \to x0} f(x) = L1$ $lim_{x \to x0} g(x) = L2$

allora

$lim_{x \to x0} (f+g)(x) = L1+L2$

Le stesse proprietà valgono per sottrazione e moltiplicazione; idem per la divisione, ma avendo l'accortezza di porre il denominatore ≠ 0

Teorema di compressione (o dei due carabinieri)

Date tre funzioni
f,g,h:A→ℝ

supponiamo

h(x)≥g(x)≥f(x) tale che x ∈ intorno I (x₀, r)

$lim_{x \to x0} f(x) = L = lim_{x \to x0} h(x)$

allora anche

$lim_{x \to x0} g(x) = L$

Esempio di teorema di compressione

Determinare il limite della funzione sen(θ)/θ non è banale.
Tramite il teorema di compressione però possiamo determinare che

cos(θ)≤sen(θ)/θ≤1

e siccome

$lim_{θ \to 0} cos(θ) = 1$

per il teorema di compressione possiamo dire che

$lim_{θ \to 0} \frac{sen(θ)}{θ} = 1$