Probabilità & statistica, Page 2 Categoria

Il problema che la distribuzione binomiale si propone di risolvere riguarda la probabilità che in una popolazione divisibile in successi e insuccessi si ottengano k successi a fronte di n estrazioni con reinserimento.

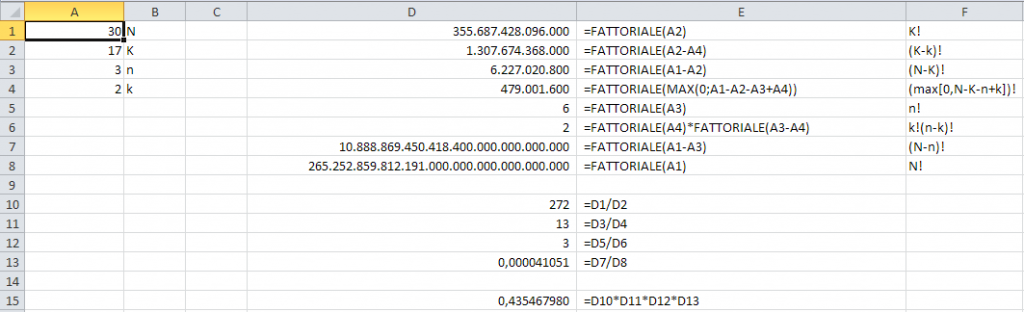
Rispetto all'esempio della distribuzione ipergeometrica, in cui a fronte di una popolazione di 30 persone di cui 17 maschi e 13 femmine, vorrei sapere la probabilità di chiamare per un'interrogazione esattamente 2 maschi su 3 persone, nella distribuzione binomiale possiamo immaginare di chiamare una sola persona per materia, interrogando 3 volte.

Di conseguenza, lo stesso studente può essere chiamato più volte e tutto il conteggio diventa molto più semplice, mentre il ragionamento sottostante è praticamente uguale.

Ho 30 studenti, 17 maschi, 13 femmine, interrogo nella prima materia: ottengo 17/30 probabilità di avere un maschio K/N contro 13/30 di avere una femmina (1-K)/N

Per la seconda e la terza materia è uguale, perché lo studente chiamato torna a posto e ritorna disponibile per un'altra interrogazione. Si può dire che le tre materie siano commutative.

La probabilità di ottenere due maschi e una femmina è il prodotto di:

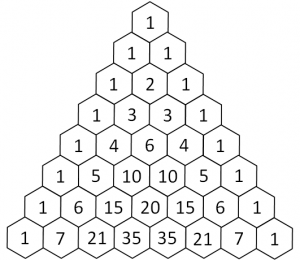
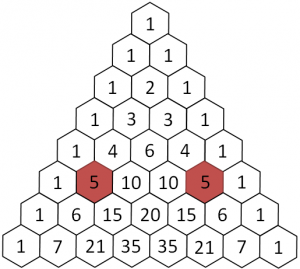
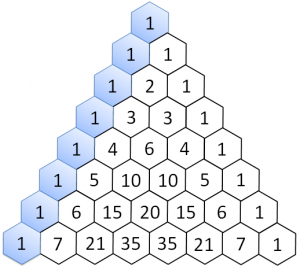
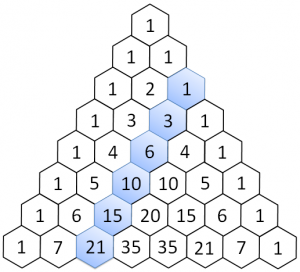
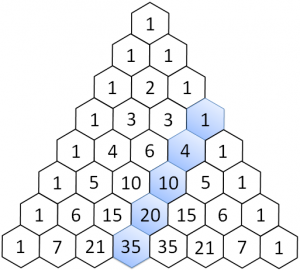
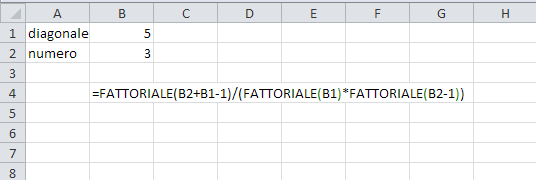
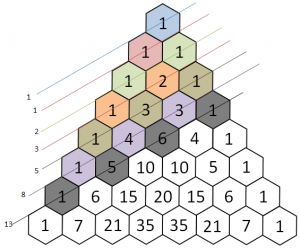
• • tre: il numero di casi in cui ho 2M e 1F: MMF, MFM, FMM, calcolato come coefficiente binomiale (2 3)
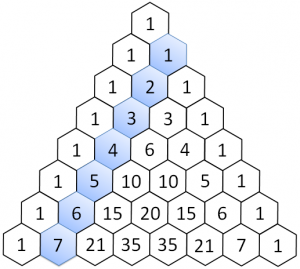
  • 17/30 ripetuto tante volte quante è richiesto un caso di successo: (17/30)²
  • 13/30 ripetuto tante volte quante è richiesto un caso di insuccesso: (13/30)¹

La formula generale "scritta bene" è quindi:

$\left(\genfrac{}{}{0ex}{}{k}{n}\right){\frac{K}{N}}^k{\frac{N-K}{N}}^{n-k}$

Scritta ancora meglio, se P = K/N, cioè P rappresenta la probabilità di successo:

$\left(\genfrac{}{}{0ex}{}{k}{n}\right)P^k{\left(1-P\right)}^{n-k}$

Il problema che la distribuzione ipergeometrica si propone di risolvere riguarda la probabilità che uno o più successi (in statistica, il "successo" non porta necessariamente una connotazione positiva) accadano in un numero di eventi in seguito a un numero di rilevazioni.

Per esempio in una popolazione di 30 studenti, di cui 17 maschi e 13 femmine siano chiamate a essere interrogate tre persone di cui esattamente due maschi.

La popolazione è indicata con N, e corrisponde, nell'esempio, a 30.

I successi sono indicati con K, e corrispondono, nell'esempio, a 2 (ovviamente si poteva scegliere di considerare "successo" anche 1, ribaltando la domanda: quante probabilità di interrogare esattamente una femmina su tre interrogati).

Il numero di rilevazioni è indicato con n ed è 3.

Notiamo che chiamando 15 persone (tutte le femmine + due maschi) non è possibile arrivare a non interrogare esattamente due maschi in nessun caso: possiamo ottenere, seppure con probabilità scarsa, fino a 13 femmine e 0 maschi oppure 14 femmine e 1 maschio, ma all'estrazione successiva restano solo maschi.

P(n = (1-K)+k) = 1.

Notiamo anche che chiamando una sola persona non possiamo ottenere sicuramente due maschi.

P(n < k) = 0

Infine il numero di estrazioni deve essere minore o uguale al numero di elementi.

n ≤ N

Alla prima chiamata, possiamo ottenere un maschio oppure una femmina

Maschio P(1) = 17/30

Femmina 1-P(1) = (30-17)/30

La seconda chiamata dipende dall'esito della prima, e questo distingue la distribuzione ipergeometrica da molte altre distribuzioni: la distribuzione ipergeometrica "ha memoria".

La seconda estrazione si fa su un campione non più di 30, ma di 29 elementi, in quanto uno (maschio o femmina che sia) è stato estratto.

Per quanto riguarda i successi, il numero di possiblità cambia in base all'estrazione precedente: 17 successi se l'estrazione precedente è stata scelta una femmina; 16 viceversa.

La probabilità di estrarre un maschio è quindi "biforcata":

Se la prima estrazione è uscito un maschio, è di 16/29, se la prima è uscita una femmina è di 17/29; quindi la probabilità di avere due maschi è di 17/30*16/29 (˜31,2%).

Sommando la probabilità che alla seconda sia uscita una femmina 13/30*13/29 (˜25,4%) e la probabilità che alla prima estrazione sia uscita una femmina 13/30 (˜43,3%), si ottiene 1: infatti è sicuro che su due estrazioni sia uscita una femmina al primo turno oppure un maschio e uno tra maschio o femmina al secondo.

Le estrazioni possono essere rappresentate come un albero binario, in cui a ogni estrazione si sceglie di seguire il percorso di sinistra in caso di successo o destra in caso di insuccesso (anche questa è una convenzione, senza considerazioni di merito).

A ogni passo dell'albero, le informazioni che cambiano sono il numero di elementi del campione (decrementa a ogni livello dell'albero), il numero di successi (si decrementa solo nel ramo di sinistra), il cumulo di percentuale di probabilità, che moltiplica le probabilità precedenti fino alla radice.

Per il nostro problema, che è di trovare la probabilità che escano due elementi maschi su tre, ci viene in aiuto il coefficiente binomiale, che ci dice che le combinazioni utili sono 1, 3, 3, 1, ovvero 1 sequenza che porta a tre maschi, 3 che portano a due maschi e una femmina, 3 a due femmine e un maschio e 1 che porta a tre femmine (1: {MMM}; 3: {MMF, MFM, FMM}; 3: {FFM, FMF, MFF}; 1: {FFF}).

Le probabilità che ci interessa contare sono quelle del secondo gruppo: MMF, MFM, FMM.

MMF:

Alla prima estrazione abbiamo 30 elementi, 17 successi, una probabilità accumulata nulla, quindi la probabilità di successo è 17/30.
Alla seconda abbiamo 29 elementi, 16 successi, una probabilità accumulata di 17/30, quindi una probabilità di successo di 16/29 * 17/30 = 272/870.
Alla terza abbiamo 28 elementi, 15 successi, una probabilità accumulata di 272/870 e dobbiamo calcolare la probabilità che esca una femmina, che è di 13/28; la probabilità di successo è quindi di 3.536/24.360.

MFM:

Prima: abbiamo 30 el, 17 succ, p.a. nulla, p(M) = 17/30.
Seconda: abbiamo 29 el, 16 succ, p.a. 17/30, ci interessa la probabilità che esca femmina, che è 13/29, il totale è 17/30*13/29 = 221/870.
Terza: abbiamo 28 el, 16 succ. p.a. 221/870, ci interessa la probabilità che esca maschio, che è 16/28, il totale è 221/870*16/28= 3.536/24.360

FMM:

Prima: abbiamo 30 el, 17 succ, p.a. nulla, p(F) = 13/30
Seconda: abbiamo 29 el, 17 succ, p.a. 13/30, P(M) = 17/29, p. tot = 221/870.
Terza: abbiamo 28 el, 16 succ. p.a. 221/870, ci interessa la probabilità che esca maschio, che è 16/28, il totale è 221/870*16/28= 3.536/24.360

Sommando tre volte 3.536 si ottiene 10.608, che diviso per 24.360 dà 0,43546...

Notiamo che la probabilità che si ottenga MMF, MFM o FMM è identica, perché anche se le percentuali di probabilità cambiano, alla fine abbiamo sempre 17, 16, 13 al numeratore e 30, 29, 28 al denominatore.

I dati che ci interessano per generalizzare la formula sono:

• 30 * 29 * 28, che è N! / (N-n)!
• 17 * 16 * 13, che è il prodotto di K! / (K-k)! e (N-K)! / (N-K-n+k)!
• 3, che è il coefficiente binomiale di (2 3), cioè i casi di successo desiderati sulle estrazioni

Il risultato è dato dal prodotto di questi termini:

$\frac{K!}{\left(K-k\right)!}$

rappresenta il numero di esiti positivi che vogliamo ottenere (nell'esempio, 17*16)

$\frac{\left(N-K\right)!}{\left(N-K-n+k\right)!}$

rappresenta il numero di esiti negativi utili a completare il numero di estrazioni (nell'esempio, 13, ma se fossero state più estrazioni sarebbero 13*12*11...)

$\frac{n!}{k!\left(n-k\right)!}$

è rappresentabile anche come

$\left(\genfrac{}{}{0ex}{}{k}{n}\right)$

è il numero di risultati corrispondenti al nostro requisito (2 maschi su 3 persone).
Da notare che il numero di femmine (1 femmina su 3 persone), cioè

$\left(\genfrac{}{}{0ex}{}{1}{3}\right)$

dà lo stesso risultato; in generale, portando il concetto in formula:

$\left(\genfrac{}{}{0ex}{}{k}{n}\right)=\left(\genfrac{}{}{0ex}{}{\mathrm{n-k}}{n}\right)$

$\frac{\left(N-n\right)!}{N!}$

è l'inverso - poiché sta al denominatore - del numero totale di esiti possibili (nel nostro esempio 1/(30*29*28)).

Moltiplicando tutto, si ottiene

$\frac{K!}{\left(K-k\right)!}\frac{\left(N-K\right)!}{\left(N-K-n+k\right)!}\frac{n!}{k!\left(n-k\right)!}\frac{\left(N-n\right)!}{N!}$

La formula è già incasinata così come sta, ma è necessario porre un'ulteriore limitazione:

$\frac{K!}{\left(K-k\right)!}\frac{\left(N-K\right)!}{\left(max\left(0,N-K-n+k\right)\right)!}\frac{n!}{k!\left(n-k\right)!}\frac{\left(N-n\right)!}{N!}$

che rappresenta il fatto che, se estraiamo 14 persone, sicuramente estraiamo almeno un maschio, N-K-n+k potrebbe essere un valore negativo.

Formula semplificata

Dopo aver "sbattuto" contro questa formula, la formula "semplificata" sembrerà quasi abbordabile, pur essendo costituita da ben tre coefficienti binomiali:

$\frac{\left(\genfrac{}{}{0ex}{}{K}{k}\right)\left(\genfrac{}{}{0ex}{}{N-K}{n-k}\right)}{\left(\genfrac{}{}{0ex}{}{N}{n}\right)}$

Basta riscrivere la formula a coefficienti binomiali come formula con i fattoriali, secondo l'equivalenza

$\left(\genfrac{}{}{0ex}{}{k}{n}\right)=\frac{n!}{k!\left(n-k\right)!}$

per ottenere praticamente la funzione da cui siamo partiti.

Excel

Di seguito, uno screenshot di un foglio excel in cui è riportato tutto il ragionamento sotto forma di formule

Calcolare velocemente distribuzioni ipergeometriche semplici

Quando un problema è posto come

c'è una popolazione di N elementi, di cui K sono successi: quante probabilità ho di ottenere k successi su n estrazioni?

sono di fronte a un problema risolvibile con la distibuzione ipergeometrica. Purtroppo il calcolo di un coefficiente binomiale come quello dell'esempio richiede di calcolare 30! e 27!, che sono numeri enormi.

È possibile calcolare il risultato di un problema abbastanza semplice ragionando in questo modo:

1. Al numeratore metto una serie discendente di numeri che rappresentano le probabilità di successo (nell'esempio 2 probabilità di successo = 17*16) e le moltiplico per la serie discendente di insuccessi, fino ad avere un prodotto di n numeri, dove n è il numero di estrazioni (nell'esempio, 17*16*13)
2. Al denominatore metto una serie discendente di popolazione, da 1 a n (nell'esempio, 30*29*28).
3. Ottengo due serie di prodotti con lo stesso numero di termini (nell'esempio, 3 termini al numeratore e 3 al denominatore: 17*16*15 / 30*29*28).
4. Moltiplico per il coefficiente binomiale, ma - se i numeri sono piccoli - posso arrivarci anche ragionando: ho 8 possibilità diverse (MMM, MMF, MFM, MFF, FMM, FMF, FFM, FFF), di cui 3 di ottenere esattamente 2 maschi e una femmina.

Variabile aleatoria

Una variabile aleatoria è una variabile il cui valore non è conosciuto a priori.

Le V.A. possono essere discrete (praticamente ℕ) o continue (praticamente ℝ⁺).

Ciascun esito può prendere un valore compreso tra 0 e 1, e la somma di tutti gli esiti fa 1. 0 = evento impossibile; 1 = evento certo. P.E. gli esiti di una moneta non truccata sono: 1/2 testa, 1/2 croce.

Spazio campionario

uno spazio campionario è un insieme di valori associati a un esito. Per es. testa = milan, croce = inter ==> milan e inter sono lo spazio campionario.

Reinserimento

Una delle caratteristiche più importanti è se ogni evento è seguito da un reinserimento oppure no.

Per esempio, il lancio di un dado genera un evento (l'uscita di un numero), ma questo non preclude che al lancio successivo possa uscire di nuovo lo stesso numero: in linea di principio potremmo avere n lanci ciascuno sempre con lo stesso numero.

L'estrazione dei numeri di una tombola, viceversa, esclude che l'evento si ripeta.

Le probabilità cambiano completamente, perché nel primo caso la probabilità per ogni evento che esca un numero è 1/6, poi al secondo evento 1/6, poi 1/6 e così via; per il secondo evento la probabilità è 1/90, poi al secondo 1/89 e così via. Quando si arriva ad avere un solo numero nel sacchetto, la probabilità che esca quel numero arriva a 1/1.

V.A. continua

Una V.A. continua è una variabile rappresentabile da un numero reale. In questo caso la probabilità è rappresentata dall'area sottostante il grafico della funzione. A differenza di una funzione generica, una funzione che esprime una probabilità è sempre non negativa; questo significa che possiamo considerare l'integrale sottostante alla stregua di una vera e propria area. Inoltre l'integrale della funzione su tutto il suo dominio ha valore 1: in altre parole, sommando tutti i valori (infiniti) che può prendere la funzione, la probabilità che un evento abbia uno di quei valori è 1 (certezza).

Può capitare che una V.A. continua sia rappresentata da una funzione che ha un certo valore k quando tende a zero, rappresentato da

$\underset{x\to 0}{\lim }f\left(x\right)=k$

e poi la funzione decresca sempre di più, in modo che

$\underset{x\to \mathrm{\infty }}{\lim }f\left(x\right)=0$

ma abbia come dominio ℝ⁺, e quindi "prosegua all'infinito". In questo caso dobbiamo utilizzare un integrale improprio, poiché il dominio non è limitato superiormente. Per esempio la funzione 1/x² ha integrale da 1 a infinito = 1 e il suo valore è sempre positivo.

Mentre la probabilità di un singolo evento è nulla, poiché ci sono infiniti eventi, la probabilità che un evento ricada tra due numeri diversi è calcolabile come area sottostante, sempre tramite l'integrale.

Per esempio, se la funzione di probabilità è rappresentata da 1/x², la probabilità che un evento accada tra x = 1 e x = 2 è data da

$\underset{1}{\overset{2}{\int }}\frac{1}{x^2}dx=-\frac{1}{2}-\left(-1\right)=\frac{1}{2}$

Funzione di ripartizione

La funzione di ripartizione restituisce la probabilità che si verifichi un evento minore o uguale a un valore dato.

Il valore cresce continuamente, perché in ogni momento la probabilità che si verifichi un evento si somma a tutte le probabilità precedenti.

Per es. la probabilità che esca un numero minore o uguale a 23 alla tombola è 23/90 (1/90 per il numero 1 + 1/90 per il numero 2 + 1/90 per il numero 3 ... + 1/90 per il numero 23).

Nel caso di una funzione continua, la funzione di ripartizione è data dall'integrale da meno infinito a x della funzione.

Valore atteso

Il valore atteso equivale alla media aritmetica.

Varianza

La varianza è un indice (un valore numerico) che indica quanto lontani sono i valori di una V.A. uno dall'altro.

Si calcola facendo la differenza tra la media dei quadrati e i quadrati della media. Una caratteristica della media dei quadrati è che è sempre maggiore del quadrato della media, quindi sottraendo la prima al secondo si ottiene un valore sempre non negativo.

La varianza è un valore che cresce esponenzialmente: quindi la differenza tra la varianza tra due valori vicini e tra due valori lontani cresce in maniera molto veloce.

P.E. la differenza tra la varianza tra 35 e 43 (media: 39, varianza: 16) e tra 34 e 44 (media: 39, varianza: 25) è minore della differenza tra la varianza tra 28 e 50 (media: 39, varianza: 121) e tra 27 e 51(media: 39, varianza: 144)

La formula per la varianza di una variabile aleatoria continua è omologa a quella discreta, ma fa uso di un integrale:

$\underset{R}{\int }{x}^{2}f\left(x\right)\mathrm{dx}-AVG{\left(x\right)}^2$

Moda

La moda è il valore più ricorrente in una V.A. discreta.

Nel caso di una V.A. continua, la moda è data dal punto (o dai punti) di massimo della funzione.

Mediana

La mediana è data dal valore intermedio in uno spazio campionario ordinato.

P.E. se lo spazio campionario è [3, 19, 32, 12, 15, 22, 7, 29, 24]

lo spazio campionario con i valori ordinati è [3, 7, 12, 15, 19, 22, 24, 29, 32]

la mediana è il valore centrale dell'elenco: 19.

Se lo spazio campionario ha un numero pari di elementi, la mediana è la media degli elementi centrali.

La mediana può essere ricavata tramite la funzione di ripartizione, ed è il minimo elemento in cui la funzione è ≥ ½.

La mediana di una V.A. continua è il punto in cui la sua funzione di ripartizione vale ½:

$\underset{R}{\int }f\left(x\right)dx=\frac{1}{2}$

Quantili

Lo stesso discorso della mediana vale per i quantili, che rappresentano altre suddivisioni dello spazio campionario: i quartili indicano una suddivisione in quattro, i centili in cento e così via.

Quando si usa

• Conosciamo la composizione della popolazione
• Si può dividere in due nettamente la popolazione
• C’è reinserimento

Esempi

Si consideri un'urna contenente quattro elementi, la cui probabilità di estrazione è

$X=\left\{\frac{1}{\mathrm{2/7}}\frac{2}{\mathrm{2/7}}\frac{3}{\mathrm{2/7}}\frac{4}{\mathrm{1/7}}\right\}$

in alternativa si possono considerare due biglie 1, due biglie 2, due biglie 3 e una sola biglia 4 (oppure 4, 4, 4, 2...).
Le biglie 1 e 2 sono bianche; le biglie 3, 4 sono rosse
Qual è la probabilità che si estragga una biglia bianca facendo 3 estrazioni?

Formula

• n = numero di estrazioni
• p = probabilità che si verifichi un successo
• X˜B_p(n, p) = distribuzione binomiale (B) per n estrazioni con p probabilità
• k = insieme di estrazioni, da 0 a n

$P\left(X=k\right)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k{\left(1-p\right)}^{n-k}$

Soluzione dell'esempio

• p = 4/7 (la probabilità che esca il bianco)
• n = 3 (il numero di estrazioni)

$P\left(S_3=2\right)=\left(\genfrac{}{}{0ex}{}{3}{2}\right){\left(\frac{4}{7}\right)}^2{\left(\frac{3}{7}\right)}^{3-2}=3*\frac{16}{49}*\frac{3}{7}\approx \mathrm{0,41982}$

Quando si usa

• Conosciamo la composizione della popolazione
• Si può dividere in due nettamente la popolazione
• Non c'è reinserimento

Esempi

Un software consiste di 12 programmi, 5 dei quali necessitano di un upgrade. Se vengono scelti a caso 4 programmi per un test. Qual è la probabilità che almeno 2 di essi siano da aggiornare? Qual è il numero medio di programmi da aggiornare tra i 4 scelti?

Formula

• X = Variabile aleatoria che conta il numero di successi
• n = numero di estrazioni
• N = numero di elementi
• K = numero di elementi "successo" (successo significa che è vero per il criterio. Per es. se cerchiamo un bug in un programma, "successo" significa che è stato trovato)
• X˜I_p(N, K, n) = distribuzione ipergeometrica (I) in N campioni di K successi per n estrazioni
• k = ciascuno dei numeri compresi tra max{0, n-(N-K)} e min{n, K}.
  max{0, n-(N-K)} significa che se faccio più estrazioni di quanti siano i casi di non-successo, sono sicuro di estrarre almeno un successo (es. bianco = successo, rosso = insuccesso; ho un'urna con 4 bianche e 5 rosse, faccio 6 estrazioni)
• min{n, K} il ragionamento è analogo

$P\left(X=k\right)=\frac{\left(\genfrac{}{}{0ex}{}{K}{k}\right)\left(\genfrac{}{}{0ex}{}{N-K}{n-k}\right)}{\left(\genfrac{}{}{0ex}{}{N}{n}\right)}$

Soluzione dell'esempio

• N = 12 (il numero di programmi della popolazione)
• n = 4 (il numero di estrazioni)
• K = 5 (il numero di successi)
• X ≥ 2 (almeno due casi di successo, richiede il maggiore/uguale)

P(X≥2) = P(X≤1) = 1 - (P(X=0) + P(X=1))

$1-\frac{\left(\genfrac{}{}{0ex}{}{5}{0}\right)\left(\genfrac{}{}{0ex}{}{\mathrm{12}-5}{4-0}\right)}{\left(\genfrac{}{}{0ex}{}{\mathrm{12}}{4}\right)}-\frac{\left(\genfrac{}{}{0ex}{}{5}{1}\right)\left(\genfrac{}{}{0ex}{}{\mathrm{12}-5}{4-1}\right)}{\left(\genfrac{}{}{0ex}{}{\mathrm{12}}{4}\right)}=1-\frac{\left(\genfrac{}{}{0ex}{}{7}{4}\right)}{\left(\genfrac{}{}{0ex}{}{\mathrm{12}}{4}\right)}-\frac{5\left(\genfrac{}{}{0ex}{}{7}{3}\right)}{\left(\genfrac{}{}{0ex}{}{\mathrm{12}}{4}\right)}$

Dal momento che un coefficiente binomiale si calcola così:

$\left(\genfrac{}{}{0ex}{}{m}{n}\right)=\frac{m!}{n!\left(m-n\right)!}$

e che

$\left(\genfrac{}{}{0ex}{}{m}{0}\right)=1$

e che

$\left(\genfrac{}{}{0ex}{}{m}{1}\right)=m$

otteniamo che

• $\left(\genfrac{}{}{0ex}{}{7}{4}\right)=35$
• $\left(\genfrac{}{}{0ex}{}{7}{3}\right)=35$
• $\left(\genfrac{}{}{0ex}{}{12}{4}\right)=495$

Con qualche passaggio otteniamo:

$1-\frac{35}{495}-\frac{5*35}{495}=\frac{19}{33}$

Mentre le variabili discrete (in cui il campione può essere solo un numero intero, come il lancio di un dado o il numero di pecore) si possono studiare una ad una, anche se il numero può velocemente diventare immenso (es. la probabilità di vincere al lotto) e il campione può essere infinito, le variabili continue hanno un tipo di infinito legato a una proprietà dell'insieme ℚ che si estende a ℝ: c'è sempre un numero tra due numeri distinti.

Per questo, gli strumenti per affrontare il calcolo delle probabilità di un evento esprimibile in modo continuo (es. la distanza tra due auto) devono essere diversi.
Un ruolo chiave ha l'integrale: se alle elementari si spiega la statistica con torte e fette (che non sono altro che integrali in coordinate polari), all'università si rispolverano quegli integrali che - o perché la funzione ha un dominio limitato o perché l'integrale è improprio, arrivano comunque ad avere una superficie di 1.

Infatti nel calcolo della probabilità una delle caratteristiche dell'integrale è che non può mai avere valori negativi. Che senso avrebbe, infatti, una probabilità negativa? Per questo è possibile considerare un integrale alla stregua di un'area - cosa che in analisi non si può fare - in cui due punti distinti x₁ e x₂ appartenenti al dominio denotano un'area che rappresenta la probabilità che l'esito della variabile sia compreso tra x₁ e x₂. Questa superficie si chiama densità di probabilità.

La funzione di ripartizione P(x) indica la probabilità da 0 a x, con x ∈ [0, 1]. Dal momento che, come già detto, la funzione integranda non può assumere mai valori negativi, la funzione di ripartizione è sempre crescente e li limite di P(x) per x tendente a -∞ è 0 e il limite per x tendente a +∞ è 1. Infine, P(x) è continua a destra.

Varianza

Parliamo di varianza. La varianza è un indice di quanto gli esiti si differenzino dalla media. Per esempio, se lancio un dado tre volte e ottengo 2, 4, 6, poi ripeto l'esperimento e ottengo 4, 4, 4, la media in entrambi i casi è 4, ma la varianza è diversa. Se sommassi semplicemente gli scarti tra la media e ciascun esito, otterrei zero in entrambi i casi (-2 + 0 + 2 e 0 + 0 + 0).
La varianza si calcola facendo la differenza tra due elementi: il primo è la somma di tutti i quadrati dell'esito per la probabilità che possa verificarsi (nel nostro esempio, 2²*1/6 + 4²*1/6 + 6²*1/6, raccogliendo 1/6 si ottiene (2² + 4² + 6²) * 1/6, cioè 56/6 = ˜9,33333. L'altro elemento è il quadrato del valore atteso.
Il valore atteso è la somma degli esiti possibili per ciascuna probabilità: 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6. In questo caso specifico, ogni esito ha una probabilità uguale a quella degli altri, quindi si può raccogliere 1/6 e scrivere (1+2+3+4+5+6)/6 = 3,5.
La varianza di questo caso è 9,33333 - 3,5 = 5,83333.

Nel caso di una variabile continua, occorre trovare la differenza tra due integrali, uno che rappresenta la superficie associata al quadrato della variabile e l'altro al quadrato di tutto l'integrale. Si ottiene questa formula:

$\underset{A}{\int }{x}^{2}f\left(x\right)\mathrm{dx}-{\left(\underset{A}{\int }xf\left(x\right)\mathrm{dx}\right)}^2$
dove A è lo spazio campionario.

Moda

La moda di una variabile aleatoria discreta è molto semplice da calcolare: è il valore (o i valori) più ricorrente.

La moda di una V.A. continua è data dal massimo assoluto (o dai massimi, se più di uno) della funzione.

Mediana e quantili

La mediana è il valore a metà dello spazio campionario. Se lo spazio è discreto ed è composto da un numero pari di elementi, se ne prende la media dei due centrali.

Esempio 1: un dado ha come esiti possibili 1, 2, 3, 4, 5, 6; la mediana è data dalla media di 3 e 4, cioè 3,5.
Esempio 2: le età dei colleghi dell'ufficio sono {24, 30, 33, 45, 55, 62, 65}. La mediana è il valore centrale (45)

Un quantile è il valore che si trova con una suddivisione diversa dalla metà. Per esempio, il percentile rappresenta ciascuno degli elementi che si trovano a cavallo tra 1/100 del campione e il campione successivo (es. il valore a metà tra 34/100 e 35/100)

Quante probabilità ci sono di fare 6 lanciando un dado non truccato una volta?

Una su sei! Questo è ovvio. E quante probabilità ci sono di fare 6 lanciandolo due volte? Se lanciandolo una volta è 1/6, lanciandolo due volte sarà 1/6 + 1/6, cioè 2/6.

E invece no. Se lanciassimo un dado sei volte, infatti, ci sarebbero 6/6 probabilità di ottenere 6, e l'esperienza ci insegna che non è così. In realtà, la probabilità di ottenere un sei lanciando un dado sei volte è un po' meno di 2/6, così come lanciandolo tre volte è minore di 3/6 e così via. In questo modo si arriva a lanciare 6 volte un dado e a ottenere una probabilità alta, ma non certa, di ottenere un sei.

OK, questo corrisponde all'esperienza, ma allora qual è il ragionamento corretto da fare?
Facendo un rapido conteggio, le probabilità che esca sei con un lancio sono 1/6 (˜0,33333):

1
2
3
4
5
6 *

Ma se lancio due dadi le probabilità che venga fuori almeno un sei sono 11/36 (˜0,30555):

1 1
1 2
1 3
1 4
1 5
1 6 *
2 1
2 2
2 3
2 4
2 5
2 6 *
3 1
3 2
3 3
3 4
3 5
3 6 *
4 1
4 2
4 3
4 4
4 5
4 6 *
5 1
5 2
5 3
5 4
5 5
5 6 *
6 1 *
6 2 *
6 3 *
6 4 *
6 5 *
6 6 *

In pratica, considero un esito positivo solo la coppia di sei, che pesa per 1/36 sugli esiti.
Cosa succede se lancio un dado tre volte? E se lo lancio 1000 volte?
Se lo lancio tre volte posso ancora contare, su 216, il numero di esiti da "scartare", che sono quelli in cui il 6 compare due o più volte, da considerare come un esito solo: 1 6 1, 1 6 2, 1 6 3, ... , 6 6 6. Ma quanti sono? Il conto diventa un po' impegnativo.

Conviene invece contare gli esiti negativi e sottrarli da 1. Così nel caso di un lancio 1/6 deriva da 1-5/6, mentre il caso di 11/36 (numero un po' più "difficile") deriva da uno meno le probabilità che NON esca il sei: 5/6 * 5/6 = 25/36.
Con tre lanci, il numero di probabilità che NON esca 6 è di 5/6 * 5/6 * 5/6 = 125/216, quindi le probabilità che esca un sei sono 1-(125/216) = 91/216 = (˜0,42130).
Con mille lanci, la probabilità che non esca mai il sei è 1 - 5^1000 / 6^1000 = 6,58800 preceduto da 80 zeri (0,00000000000000000000000000000000000000000000000000000000000000000000000000000000658800).
Improbabile, ma non impossibile.

Concludo con una considerazione. Il lancio delle monete non ha memoria, per cui l'esito precedente non influenza in alcun modo quello successivo. Ma in questo ragionamento, il fatto che esca un sei al primo lancio influenza l'esito del lancio successivo: se esce sei, il secondo lancio è ininfluente!

1 => 1/6 di probabilità che tra il primo e il secondo lancio esca almeno un 6
2 => 1/6 di probabilità che tra il primo e il secondo lancio esca almeno un 6
3 => 1/6 di probabilità che tra il primo e il secondo lancio esca almeno un 6
4 => 1/6 di probabilità che tra il primo e il secondo lancio esca almeno un 6
5 => 1/6 di probabilità che tra il primo e il secondo lancio esca almeno un 6
6 => 1 di probabilità (100%) che tra il primo e il secondo esca almeno un 6

Esercizi per il corso di Probabilità e Statistica

Foglio 1: Statistica descrittiva

Esercizio 1

Per ognuna delle seguenti variabili si dica se si tratta di una variabile quantitativa (discreta o continua) o qualitativa (nominale o ordinale):

1. l'età degli studenti in questo corso;
2. i programmi preferiti dalle studentesse di questo corso;
3. il numero degli studenti di questo corso che guardano la trasmissione "X Factor";
4. le spese di trasporto sostenute dagli studenti di questo corso;
5. il voto riportato all'esame di matematica;
6. l'aver superato l'esame di matematica.

Risposte

1. continua
2. nominale
3. discreta
4. discreta
5. discreta

Esercizio 2

Il docente di un corso universitario ha raccolto alcuni dati sugli studenti che hanno sostenuto il suo esame. La tabella riporta i dati relativi ai primi quattro studenti.

1. Qual è l'unità statistica? Qual è la popolazione di riferimento?
2. Quali caratteri (variabili) sono rilevati?
3. Quali sono le modalità rilevate del Diploma Superiore?
4. Quali sono le modalità rilevate del Voto e quali quelle possibili?

Risposte

1. L'unità statistica è lo studente e la popolazione è l'insieme degli studenti che hanno superato l'esame.
2. Sono rilevati il voto, l'anno di corso, la residenza e il diploma di scuola superiore
3. Le modalità rilevate del diploma superiore sono: Liceo S, Ist. Tecnico N, Ist. Comm. S, Ist. Prof. S...
4. Le modalità rilevate del voto sono ins, 18, 19, 20,... 30, 30L (non è specificato che l'esame sia superato)

Esercizio 3

In un gruppo di 20 persone sono state rilevate due variabili, il sesso e l'età

47 61 38 40 26 41 49 65 53 55
F  M  M  M  F  M  F  F  M  F
30 23 34 33 40 21 65 32 47 50
M  F  M  F  M  M  M  F  F  F

1. Si costruisca la distribuzione per classi dell'età (utilizzando le classi 19-29, 30-44, 45-59, 60 e oltre) e si calcolino le frequenze assolute, relative, percentuali, le cumulate e le densità di frequenza. Si disegni un opportuno istogramma.
2. Si rappresenti la funzione di ripartizione empirica e se ne calcoli il valore nel
   punto 57.
3. Si disegni il diagramma a scatola con baffi, partendo dai dati originari.
4. Si calcolino media, varianza, scarto quadratico medio, campo di variazione,
   scarto interquantile e coefficiente di variazione.
5. Si chiamino yi i valori originari e zi quelli standardizzati: si trovino media e
   varianza degli zi attraverso le corrispondenti quantità degli yi.

Risposte

1. 	freq. ass	f. rel.	%	ass. cum	rel. cum	dens.
   19-29	3	0,15	15	3	0,15	0,3
   30-44	8	0,4	40	11	0,55	˜0,57
   45-59	6	0,3	30	17	0,85	˜0,43
   60+	3	0,15	15	20	1	0,6

   Grafico:

   

2. Grafico della ripartizione empirica:
   
   Ripartizione empirica = frequenza relativa di unità con valore ≤ x.
   La ripartizione empirica di 57 è 0,85.
3. Grafico:
   
   
4. Dati A = l'insieme dei valori; n = il numero di elementi in A; A(i) l'i-esimo elemento di A (i ∈ ℕ):
   • media
     $\frac{\sum _{i=1}^{n}A\left(i\right)}{n}$Usando R, si ottiene che mean(A) = 42,5
   • varianza
     $\frac{\sum _{i=1}^n{\left(A\left(i\right)-media\left(A\right)\right)}^2}{n}$La media dei quadrati è 1973,2, il quadrato della media è 1806,25, quindi la varianza è 166,95
   • scarto quadratico medio (radice della varianza): ˜12,92
   • campo di variazione: la differenza tra il valore più alto (65) e il più basso (21): 65-21 = 44
   • scarto interquantile: differenza tra il terzo e il primo quartile. [21 23 26 30 32] [33 34 38 40 40] [41 47 47 49 50] [53 55 61 65 65] 50-32 = 18
   • coefficiente di variazione ⇒?

Esercizio 4

L'assistenza tecnica di un rivenditore di computer ha registrato le richieste di intervento in un particolare giorno. Il risultato è stato:

H,H,M,S,H,M,M,S,H,S,S,M,H,M,M,S,M

dove H=problemi hardware, S=problemi software, M=guasto monitor.

1. Calcolare la distribuzione delle frequenze assolute e relative; disegnare il diagramma a barre;
2. calcolare un indice di posizione opportuno

Risposte

1. 	F. ass.	F. rel
   H	5	˜0,29
   S	5	˜0,29
   M	7	˜0,41

2. L'indice di posizione opportuno è la moda, il cui valore è M (guasto al monitor)

Esercizio 5

Nella tabella sottostante sono riportati i consumi (in milioni di tonnellate) di risorse naturali impiegate nell'economia italiana nel quinquennio 2000-2004 e le importazioni delle medesime risorse nello stesso arco temporale.

             2000     2001     2002       2003     2004
Fabbisogno      2.357    2.295    2.214      2.077    2.184
Importazioni  329.028  330.035    334.807  343.784  360.282

1. Si rappresentino graficamente i dati;
2. si calcolino la covarianza e il coefficiente di correlazione e si dia un'interpretazione dei risultati.

Esercizio 6

Il responsabile della sicurezza di una grossa azienda ha rilevato il numero di tentativi di intrusione bloccati ogni giorno durante i primi 14 giorni del mese:

56 47 49 37 38 60 50 43 43 59 50 56 54 58

Dopo aver cambiato le impostazioni del firewall, le intrusioni bloccate nei 20 giorni
successivi sono state

53 21 32 49 45 38 44 33 32 43 53 46 36 48 39 35 37 36 39 45

Al fine di valutare l'efficacia delle nuove impostazioni, si confrontino il numero di tentativi di intrusione bloccati prima e dopo il cambio, calcolando il summary dei dati, tracciando i boxplot appaiati e commentando i risultati ottenuti.

Esercizio 7

I dati seguenti rappresentano il numero di registrazioni di nuovi account in dieci giorni consecutivi ad un sito di vendite online:

43 37 50 51 58 105 52 45 45 10

1. Calcolare media, mediana, quartili e deviazione standard.
2. Trovare gli outlier (osservazioni anomale) usando la regola 1:5Xdistanza interquartile.
3. Eliminare gli outlier trovati e calcolare nuovamente media, mediana, quartili e scarto quadratico medio.
4. Trarre delle conclusioni sull'influenza degli outlier sugli indici calcolati.

Esercizio 8

Un provider vuole valutare il carico della sua rete e registra il numero di utenti (in migliaia di persone) connessi contemporaneamente in 50 luoghi:

17.2 22.1 18.5 17.2 18.6 14.8 21.7 15.8 16.3 22.8
24.1 13.3 16.2 17.5 19.0 23.9 14.8 22.2 21.7 20.7
13.5 15.8 13.1 16.1 21.9 23.9 19.3 12.0 19.9 19.4
15.4 16.7 19.5 16.2 16.9 17.1 20.2 13.4 19.8 17.7
19.7 18.7 17.6 15.9 15.2 17.1 15.0 18.8 21.6 11.9

1. Calcolare la media campionaria, la varianza e lo scarto quadratico medio dei dati rilevati.
2. Calcolare il summary e costruire il boxplot.
3. Calcolare lo scarto interquantile. Sono presenti delgli outliers?
4. Tracciare un istogramma e commentare la simmetria della distribuzione.

Ω

Ω rappresenta l'insieme dei possibili risultati. La probabilità di tutti gli eventi che appartengono a Ω è 1.

ω

ω rappresenta un elemento dell'insieme Ω, cioè l'esito di un singolo evento.

$\stackrel{\mathrm{----}}{\Omega }$

$\stackrel{\mathrm{----}}{\Omega }$ è l'insieme complementare di Ω, cioè un evento impossibile. Qualunque insieme con una "barretta" sopra è l'insieme degli esiti diversi dall'insieme rappresentato. Si può rappresentare anche con 1 - P(A), cioè 1 meno la probabilità che si verifichi un evento di A

P(A)

P(A), con A ⊆ Ω è la probabilità che si verifichi uno degli eventi dell'insieme A.

P(A_i) è la probabilità che si verifichi l'i-esimo elemento dell'insieme A. A volte, senza tirare in ballo l'insieme A, si indica con p_i