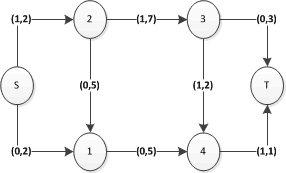
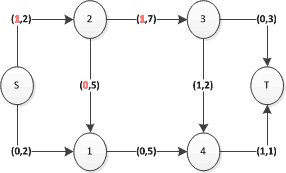
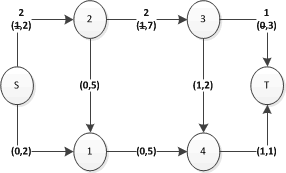
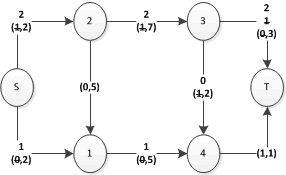
Il knapsack in pratica
Risolviamo il seguente problema:
| max | 4x1 | +2x2 | +3x3 | -5x4 | -x5 | +x6 | |
| 3x1 | -3x2 | +x3 | +x4 | -x5 | ≤1/2 |
x∈{0,1}6
La prima riga è il problema, ed è rappresentato dalla formula
per j = 1, cj = 4
per j = 2, cj = 2
eccetera
La seconda riga è il vincolo, ed è rappresentato dalla formula
per j = 1, aj = 3
per j = 2, aj = 3
per j = 3, aj = 1
eccetera
infine, b = 1/2
Riepiloghiamo le prime semplificazioni possibili in questo prospetto:
| c < 0 | c = 0 | c > 0 | |
| a < 0 | xj = 1 - yj | 1 | 1 |
| a = 0 | 0 | 0 | 1 |
| a > 0 | 0 | 0 | xj |
Nell'esempio:
- c>0, a>0
- c>0, a<0 => x2 = 1
- c>0, a>0
- c<0, a>0 => x4 = 0
- c<0, a<0 => x5 = 1-y5
- c>0, a=0 => x6 = 1
Sostituendo nel problema i valori noti e la sostituzione di x5, otteniamo
| max | 4x1 | +2*1 | +3x3 | -5*0 | -(1-y5) | +1 | |
| 3x1 | -3 | +x3 | -(1-y5) | ≤1/2 |
con 0 ≤ x1, x3, y5 ≤ 1
il problema si può riscrivere come
| max | 4x1 | +3x3 | +y5 | +2 |
| 3x1 | +x3 | +y5 | ≤9/2 |
A questo punto, bisogna ordinare le variabili in base al rapporto tra c e a: 4/3, 3/1, 1/1.
e bisogna verificare quanti di questi numeri ∈ℚ, sommati tra loro nell'ordine, sono minori o uguali di 4,5.
3 < 4,5
3 + 4/3 < 4,5
3 + 4/3 + 2 > 4,5
quindi il nostro indice è 2.
x1, a cui corrisponde la frazione 4/3, vale 1
x3, a cui corrisponde 3, vale 1
y5, a cui corrisponde l'ultimo 1, vale
quindi
Se y5 = 0,5 allora x5 = 1-0,5 = 0,5
La soluzione è quindi x1 = 1; x2 = 1; x3 = 1; x4 = 0; x5 = 0.5; x6 = 1;