Simplesso = Complesso?

Il punto di vista geometrico della soluzione di problemi

Quando in un problema di programmazione lineare (PL) sono presenti solo due variabili, il problema può essere descritto come una superficie di un piano. Per esempio:

$\{\begin{array}{c}{x}_1>2\\ x_1+x_2\ge 5\\ x_2\le 9\end{array}$

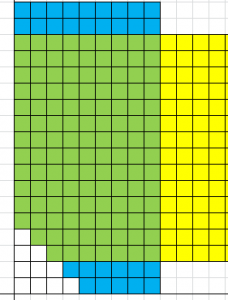
Le soluzioni ottimali si trovano agli angoli della regione ammissibile (es. trovare i valori massimi possibili di x₁ e x₂), se esistono più soluzioni ammissibili (es. trovare i valori minimi possibili di x₁ e x₂) sono sempre vertici adiacenti.

Se le variabili sono più di due, rappresentare il problema graficamente è molto più difficile, perché nel caso di tre variabili servirebbe un solido, mentre nel caso di quattro o più variabili non sarebbe possibile una rappresentazione grafica unica di tutto il problema.

Il metodo del simplesso

Quando le dimensioni diventano tante, un approccio geometrico diventa più difficile di uno algebrico. Per risolvere un problema a più dimensioni, si comincia considerando il punto (0, 0, ...0), cioè l'origine, una volta che le variabili sono trasformate in modo da poter assumere solo valori positivi.

Successivamente, verificato che il punto di origine non è una soluzione ottima, ci si sposta al vertice adiacente più lontano, in modo da massimizzare il risultato del primo passaggio.

Arrivati al punto successivo, si ripete l'operazione finché tutti i vertici adiacenti non sono soluzioni peggiori di quella individuata.

Un esempio

Si risolva questo problema:

max Z = 3x1 + 5x2

con i segenti vincoli
x1        ≤ 4
      2x2 ≤ 12
3x1 + 2x2 ≤ 18
x1, x2 ≥ 0

Per risolvere il problema è necessario introdurre delle variabili per cui le disequazioni diventino equazioni, per esempio, per quanto riguarda il primo vincolo, x₁ ≤ 4 diventa x₁ + x₃ = 4, dove evidentemente x₃ = 4 - x₁

Il problema ora si può riscrivere così (forma aumentata):

x1        + x3         = 4
      2x2     + x4     = 12
3x1 + 2x2          + x5 = 18
x1, x2, x3, x4, x5 ≥ 0

Ponendo via via le variabili uguali a zero, si ottengono i vertici del poliedro.
x₁ = 0, x₄ = 0: (0,6,4,0,6)

x₃ = 0, x₄ = 0: (4,6,0,0,-6) vertice non ammissibile, perché una delle variabili è negativa

x₁ = 0, x₂ = 0: (0,0,4,12,18)

x₃ = 0, x₂ = 0: (4,0,0,12,6)

x₄ = 0, x₅ = 0: (2,6,2,0,0)

x₃ = 0, x₅ = 0: (4,3,0,6,0)

Iniziando dal vincolo x₁ = 0, x₂ = 0 si ottiene un vertice ammissibile, ma certamente non è la soluzione migliore, perché Z = 0.

Provando a muoversi lungo le due direzioni adiecenti al vertice (0,0), scegliamo la direzione dove il tasso di miglioramento è maggiore, quindi manteniamo x₁ a zero e portiamo x₂ al suo valore massimo ammissibile (cioè poniamo x₄ a zero):

x₁ = 0, x₄ = 0: (0,6,4,0,6), Z = 30

A questo punto, essendoci solo due variabili, è possibile tentare di migliorare Z solo in una direzione, cioè (2, 6).

Con x₁ = 2, x₂ = 6 il risultato Z = 36, che è sicuramente migliore del 30 di x₁ = 0, x₂ = 6. Come faccio a sapere se il risultato si può migliorare? Tento di spostarmi ancora, e mi sposto al vertice successivo, che è x₁ = 4, x₂ = 3. In questo caso, Z = 27, che è un risultato peggiore del precedente.

Siccome il problema è convesso, non è possibile che esistano soluzioni migliori di quella che si trova vicino solo vertici peggiori, quindi la soluzione al mio problema è x₁ = 2, x₂ = 6 (e, per completezza, x₃ = 2, x₄ = 0, x₅ = 0).

Il metodo del simplesso (forma tabellare)

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18

I dati riportati in questa tabella rappresentano il problema (prima riga) e i vincoli (le tre righe successive), sotto forma di coefficienti delle variabili.

Il problema è Z-3x₁-5x₂ = 0, per questo le variabili della prima riga sono scritte con segno negativo. La variabile di base (quella di cui vogliamo conoscere il valore) è Z.

Nelle righe successive, le variabili di base corrispondono alle variabili slack, cioè a quelle introdotte per ottenere il termine noto nel caso in cui le variabili non di base non fossero sufficienti.

Test di ottimalità: è soddisfatto solo se tutti i termini della prima riga sono non negativi. In questo caso non lo sono.

Iterazione: scegliere nella prima riga il coefficiente più basso (il più alto, in valore assoluto): in questo esempio è x₂ = -5.

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18

Tra gli elementi della colonna, scegliere il più piccolo dei valori non negativi:

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12/2 = 6
x5	(3)	0	3	2	0	0	1	18/2 = 9

Abbiamo identificato la variabile uscente (x₂) e la variabile entrante (x₄).
Ora otteniamo la nuova riga pivot dividendo tutta la riga per l'elemento pivot.

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18
Z	(0)	1
x3	(1)	0
x2	(2)	0	0	1	0	½	0	6
x5	(3)	0

N.B. per forza se divido il coefficiente trovato per il coefficiente, otterrò uno (cella x₂/x₂).

Ora valutiamo le righe della colonna pivot: se sono positive, sottrarre, altrimenti sommare il prodotto tra il coefficiente (valore assoluto) e la nuova riga pivot.

N.B. per forza, la prima riga della colonna pivot finisce a zero.

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18
Z	(0)	1	-3 + (0*5)	-5 + (1*5)	0 + (0*5)	0 + (½ * 5)	0 + (0*5)	0 + (6*5)
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x5	(3)	0	3 - (0*2)	2 - (1*2)	0 - (0*2)	0 - (½ * 2)	1 - (0*2)	18 - (6*2)

Svolgendo tutti i calcoli:

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18
Z	(0)	1	-3	0	0	5/2	0	30
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x5	(3)	0	3	0	0	-1	1	6

Nell'iterazione successiva:

1. Scelgo la variabile (nel tableau ricalcolato) con il coefficiente più basso (più alto in valore assoluto), che è x₁ = -3
2. Per ciascun valore della colonna scelta, divido il termine noto per il coefficiente e - solo per i valori positivi (zero escluso!) - scelgo quello più piccolo. Nell'esempio è la riga (3).
3. Scambio la variabile entrante e quella uscente e divido per la variabile pivot
4. Ricalcolo le altre righe in base alla variabile pivot e alla riga appena ricalcolata al punto precedente

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18
Z	(0)	1	-3	0	0	5/2	0	30
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x5	(3)	0	3	0	0	-1	1	6
Z	(0)	1	-3	0	0	5/2	0	30
x3	(1)	0	1	0	1	0	0	4 ⇒ 4/1 = 4
x2	(2)	0	0	1	0	½	0	6 ⇒ 6/0 no
x5	(3)	0	3	0	0	-1	1	6 ⇒ 6/3 = 2

Scelgo la terza riga

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18
Z	(0)	1	-3	0	0	5/2	0	30
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x5	(3)	0	3	0	0	-1	1	6
Z	(0)	1	-3	0	0	5/2	0	30
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x5 x1	(3)	0/3 = 0	3/3 = 1	0/3 = 0	0/3 = 0	-⅓ = -⅓	⅓ = ⅓	6/3 = 2

Aggiungo (o tolgo) il termine pivot diviso ogni elemento della riga dalla riga (0)

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18
Z	(0)	1	-3	0	0	5/2	0	30
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x5	(3)	0	3	0	0	-1	1	6
Z	(0)	1	-3 + (3*1)	0+(3*0)	0+(3*0)	5/2+(3*-⅓)	0+(3*⅓)	30+(3*2)
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x1	(3)	0	1	0	0	-⅓	⅓	2

Tolgo la riga pivot dalle altre righe

Variabili di base	Equazione	Coefficiente di						Termini noti
		Z	x1	x2	x3	x4	x5
Z	(0)	1	-3	-5	0	0	0	0
x3	(1)	0	1	0	1	0	0	4
x4	(2)	0	0	2	0	1	0	12
x5	(3)	0	3	2	0	0	1	18
Z	(0)	1	-3	0	0	5/2	0	30
x3	(1)	0	1	0	1	0	0	4
x2	(2)	0	0	1	0	½	0	6
x5	(3)	0	3	0	0	-1	1	6
Z	(0)	1	0	0	0	3/2	1	36
x3	(1)	0	1-1	0-0	1-0	0+⅓	0-⅓	4-2
x2	(2)	0	0	1	0	½	0	6
x1	(3)	0	1	0	0	-⅓	⅓	2

A questo punto nella riga (0) ci sono solo valori non negativi, quindi mi posso fermare.
Nella riga (0) c'è il valore di Z (=36) e nelle righe (3) e (2) i valori rispettivamente di x₁ (=2) e x₂ (=6).