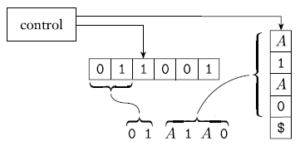
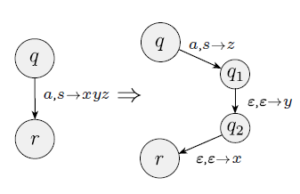
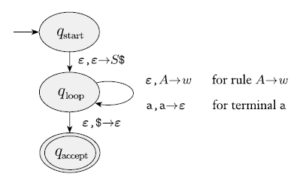
exercise 2.16
Show that the class of context-free languages is closed under the regular operations, union, concatenation, and star.
After the meeting with Calzavara, we'll rewrite the proofs using the grammars instead of PDAs
Union
Let A, B be CFLs, then exist G, H CFGs when L(G) = A and L(H) = B. Let S1, S2 the start symbols for G and H.
We can build a new CFG with start symbol S where S → S1 | S2, including all the productions of G and H.
Before the union, we must ensure that the terminals in G and H are different, by replacing the common names.
Concatenation
Let A, B be CFLs, then exist G, H CFGs when L(G) = A and L(H) = B. Let S1, S2 the start symbols for G and H.
We can build a new CFG with start symbol S where S → S1 S2, including all the productions of G and H.
As the union, we must ensure that the terminals in G and H are different.
Star
Let A be CFL, then exist G CFG when L(G) = A. Let S1 the start symbols for G.
We can build a new CFG with start symbol S where S → S S1|ε, including all the productions of G.
ε warrantees that the recursion ends and that the new CFG accepts an empty string.
OLD VERSION
Union
Proof idea
Union of two PDAs can be similar to the union of two NFA: a new start state points to both the old start states with an ε arrow. What about the stack? Since it's empty - by definition of PDA - at the new start state, the two arrows must not read or write anything from the stack, to be sure to keep the old starts states with an empty stack.
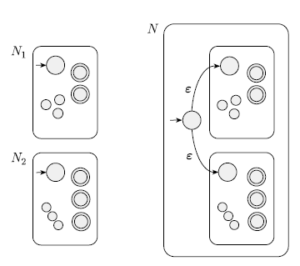
Proof
Let be A1, A2 two context-free languages. If A1 and A2 are context-free, there exists two CFG N1, N2 that recognize them. We define N1, N2 as follow:
N1 = {Q1, Σ, Γ1, δ1, q1-start, F1⊆Q1}
N2 = {Q2, Σ, Γ2, δ2, q2-start, F2⊆Q2}
Construct N that recognize A1 ∪ A2 as
N = {Q, Σ, Γ, δ, qstart, F⊆Q}
where
Q = Q1 ∪ Q2 ∪ qstart
Γ = Γ1 ∪ Γ2
qstart = "new" start state for N
F = F1 ∪ F2
δ = (for a ∈ Σ and b ∈ Γ)
- δ(q1, a, b) if q ∈ Q1
- δ(q2, a, b) if q ∈ Q2
- {q1, q2} if q = qstart and a = ε
- ∅ if q = qstart and a ≠ ε
Note that the stack is managed independently for each automaton N1 and N2
Concatenation
Proof idea
As for the union, we can start our proof using the concatenation proof for the NFAs, that consists in linking all the final states of the "first" NFA to the start state of the "second".
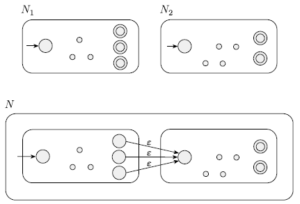
Can we be sure that at the final state the stack is empty in every case? That's an open question.
If yes, the proof idea is completed.
If not, we must add a state that loops the stack in order to empty it. This state, accepting an empty string, reads all the symbols in Γ except $, where $ is the placeholder for the end of the stack, and then goes to the next PDA where the stack contains $. This is a little tricky, but guarrantees that the stack is empty when the second PDA starts.
Proof
Let be A1, A2 two context-free languages. If A1 and A2 are context-free, there exists two CFG N1, N2 that recognize them. We define N1, N2 as follow:
N1 = {Q1, Σ, Γ1, δ1, q1-start, F1⊆Q1}
N2 = {Q2, Σ, Γ2, δ2, q2-start, F2⊆Q2}
Construct N that recognize A1 ○ A2 as
N = {Q, Σ, Γ, δ, qstart, F⊆Q}
where
Q = Q1 ∪ Q2 ∪ qdiscard
Γ = Γ1 ∪ Γ2
qstart = q1-start
F = F2
δ = (for a ∈ Σ and b ∈ Γ)
- δ(q1, a, b) if q ∈ Q1 and q ∉ F
- δ(q1, a, b) if q ∈ Q1 and q ∈ F and a ≠ ε
- δ(q1, a, b) ∪ qdiscard if q ∈ Q1 ∪ qdiscard and a = ε and b ≠ $
- q2-start if q ∈ Q1∪ qdiscard and a = ε and b = $
- δ(q2, a, b) if q ∈ Q2
Star
Proof idea
As for the union, we can start our proof using the star proof for the NFAs, that consists in:
- create a new start state (accepted) that goes to the old start state with a ε arrow
- create one ε arrow for each accepted state to the old start state
As for the concatenation, we must be sure that the stack is empty before go to the old start state again.
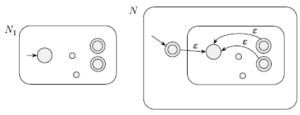
So, before return to the old start state we must add a new state qdiscard that reads all the symbols in Γ except $.
Proof
Let be A1 a context-free language. If A1 is context-free, there exists a CFG N1 that recognize it. We define N1 as follow:
N1 = {Q1, Σ, Γ1, δ1, q1-start, F1⊆Q1}
Construct N that recognize A1* as
N = {Q, Σ, Γ, δ, qstart, F⊆Q}
where
Q = Q1∪ qstart
Γ = Γ1
qstart is the new start
F = F1∪ qstart
δ = (for a ∈ Σ and b ∈ Γ)
- δ(q1, a, b) if q ∈ Q1 and q ∉ F
- δ(q1, a, b) if q ∈ Q1 and q ∈ F and a ≠ ε
- δ(q1, a, b) ∪ qdiscard if q ∈ Q1 ∪ qdiscard and a = ε and b ≠ $
- q2-start if q ∈ Q1∪ qdiscard and a = ε and b = $
- ∅ if q = qstart and a ≠ ε