Equivalenza tra PDA e Grammatiche Context Free (CFG)

Traduzione non autorizzata delle pagine del capitolo 2.2 di Sipser. In blu, i miei commenti.

In questa sezione mostriamo che le grammatiche context-free e gli automi pushdown sono equivalenti nelle loro potenzialità. Entrambi sono in grado di descrivere la classe dei linguaggi context-free. Mostriamo come convertire ogni grammatica context-free in un automa pushdown che riconosce lo stesso linguaggio e viceversa. Ricordiamo che abbiamo definito un linguaggio context-free come un linguaggio che può essere descritto con una grammatica context-free, il nostro obiettivo nel teorema seguente.

2.20 Teorema

Un linguaggio è context-free se e solo se un automa pushdown lo riconosce.

Come sempre, quando c'è un "se e solo se" in un teoriema, abbiamo due direzioni da provare. In questo teorema entrambe le direzioni sono interessanti (=incasinate). Prima, facciamo la direzione "se", più facile.

2.21 Lemma

Se un linguaggio è context-free, allora un automa pushdown lo riconosce.

Idea

Sia A un CFL. Dalla definizione, sappiamo che A ha una CFG, G, che lo genera. Mostriamo come convertire G in un PDA equivalente, che chiamiamo P.

Il PDA P che ora descriviamo accetta i suoi input w, se G genera questo input, determinando se c'è una derivazione per w. Ricordiamo che una derivazione è semplicemente la sequenza di sostituzioni fatte allo stesso modo in cui una grammatica genera una stringa. Ogni passo della derivazione produce una stringa intermedia di variabili e terminali. Disegnamo P per determinare se qualche serie di sostituzioni, usando le regole di G, possono condurre dalla variabile di partenza a w.

Una delle difficoltà nel testare se c'è una derivazione per w è immaginare quali sostituzioni fare. Il nondeterminismo del PDA permette di indovinare la sequenza di sostituzioni corrette. A ogni passaggio della derivazione, una delle regole per una variabile particolare è selezionata nondeterministicamente e usata per sostituire questa variabile.

Il PDA P inizia scrivendo la variabile di partenza nel suo stack. Passa attraverso una serie di stringhe intermedie, facendo una sostituzione dopo l'altra. Eventualmente può arrivare a una stringa che contiene solo simboli terminali, che significa che ha usato la grammatica per derivare la stringa (bingo!). Allora P accetta se la stringa è identica a quella che ha ricevuto in input.

Implementare questa strategia su un PDA richiede un'idea addizionale. Abbiamo bisogno di vedere come il PDA memorizza la stringa intermedia per andare da una a un'altra. Usare semplicemente lo stack per memorizzare ogni stringa intermedia è una tentazione. Però questo non funzione bene, perché il PDA ha bisogno di trovare la variabile nella stringa intermedia e fare sostituzioni. Il PDA può accedere solo al simbolo in cima allo stack e che può essere un simbolo terminale dentro una variabile. Il modo per aggirare il poblema è tenere solo una parte della stringa intermedia nello stack: i simboli con cui inizia la prima variabile nella stringa intermedia. Ogni simbolo terminale che appare prima della prima variabile è messa in corrispondenza immediatamente con i simboli nella stringa di input. La figura seguente illustra il PDA P.

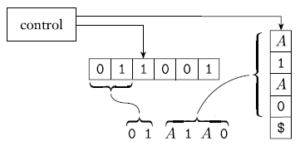
Di seguito, una descrizione informale di P.

1. Metti il simbolo marcatore $ e la variabile di partenza nello stack
2. Ripeti i seguenti passi all'infinito
   1. se la cima dello stack è una variabile simbolo A scegliere nondeterministicamente una delle regole per A e sostituire A con la stringa sul lato destro della regola
   2. se la cima dello stack è il simbolo terminale a, leggere il simbolo successivo dall'input e confrontarlo con a. Se è lo stesso, ripetere. Se non è lo stesso, rigettare questo ramo del nondeterminismo
   3. se la cima dello stack è il simbolo terminale $, entrare nello stato accettato. Facendo così, si accetta l'input se è stato letto interamente.

Qui manca un esempio, perché non si capisce molto.

Immaginiamo un PDA fatto così:

S → aAb

A → # | aAa

La stringa aa#ab è riconosciuta? Servono alcuni passaggi: aaAab (A = #), aAb (A = aAa), S (S = aAb), per cui va mantenuta la stringa intermedia.

1. metto nello stack il simbolo di dollaro $ seguito da aAb, cioè la variabile di partenza, esclusi i terminali a destra. Il mio stack contiene $aA, e siccome è una LIFO, estraggo nell'ordine Aa$
2. la cima dello stack è una variabile, quindi nondeterministicamente sostituisco A con # e aAa in due diversi branch
   1. # ⇒ nello stack ho #a$, ma quando confronto a#b con la mia stringa, ottengo una differenza, poiché il secondo carattere non è # ma a
   2. aAa => nello stack ho aAaa$, quindi la mia stringa completa è aaAab, ma quando vado a ricontrollarla sostituisco nondeterministicamente A con # e con aAa
      1. # ⇒ ottengo aa#ab, che è la mia stringa
      2. aAa ⇒ scarto questa opzione perché otterrei aaaAaab, ma il terzo carattere è # e non a.

Non ho capito ancora in che modo funziona lo scarico/carico dello stack.

Prova

Ora diamo un dettaglio formale della costruzione dell'automa pushdown P = (Q, Σ, Γ, δ, q₁, F) . Per fare una costruzione più chiara, usiamo l'abbreviazione per la funzione di transizione. QUesta notazione fornisce un modo per scrivere una stringa intera nello stack in un passaggio della macchina. Possiamo simulare questa azione introducendo degli stati addizionali per scrivere la stringa un simbolo alla volta, come implementato nella seguente costruzione formale.

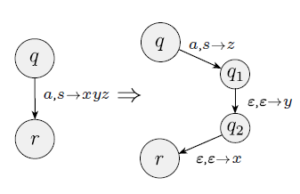
Siano q e r stati del PDA e sia a in Σ_ε e s sia in Γ_ε. Vogliamo che il PDA vada da q a r e legge a ed estrae s. Inoltre vogliamo che allo stesso tempo si spinga la stringa intera u = u₁...u_l nello stack. Possiamo implementare questa azione introducendo dei nuovi stati q₁, ..., q_l-1 e impostando la funzione di transizione in questo modo:

δ(q, a, s) per contenere (q₁, u_l),
δ(q₁, ε, ε) = {(q₂, u_l-1)},
δ(q₂, ε, ε) = {(q₃, u_l-2)},
δ(q₃, ε, ε) = {(q₄, u_l-2)},
...
δ(q_l-1, ε, ε) = {(r, u₁)}.

Usiamo la notazione (r, u) ∈ δ(q, a ,s) per dire che quando q è lo stato dell'automa, a è il prossimo simbolo di input, s è il simbolo in cima allo stack, il PDA può leggere la a e prelevare la s, allora inserisce la stringa u nello stack e va allo stato r. La figura seguente mostra questa implementazione:

Gli stati di P sono Q = {q_start, q_loop, q_accept} ∪ E, dove E è l'insieme di stati di cui abbiamo bisogno per implementare la scorciatoria appena descritta. Lo stato di inizio è q_start. L'unico stato accettato è q_accept.

La funzione di transizione è definita di seguito. Cominciamo inizializzando lo stack perché contenga i simboli $ e S, implementando il passo 1 nella descrizione informale: δ(q_start, ε, ε) = {(q_loop, S$)}. Poi facciamo le transizioni per il ciclo principale del passo 2.

Prima ci occupiamo del caso (a), se la cima dello stack contiene una variabile. Sia δ(q_loop, ε, A) = {(q_loop, w) | dove A → w è una regola in R}.

Secondo, gestiamo il caso (b), se la cima dello stack contiene un terminale. Si ha che δ(q_loop, a, a) = {(q_loop, ε)}.

Infine, gestiamo il caso (c), se il marcatore di stack vuoto $ è in cima allo stack. Si ha che δ(q_loop, ε, $) = {(q_accept, ε)}.

Il diagramma di stato è mostrato nella figura 2.24.

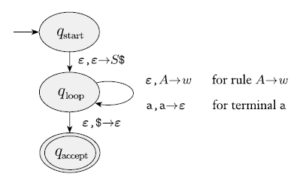
Questo completa la prova del lemma 2.21.

La seconda parte la farò se e quando lo riterrò utile