exercise 1.49

a. Theorem

Let B = {1^ky|y∈{0,1}* and y contains at least k 1s, for k ≥ 1}. Show that B is a regular language.

a. Proof

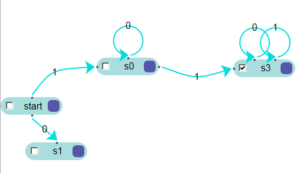
B equals to "Let B is a string that begins with 1 and, after, contains at least another 1".

This DFA doesn't "count" the number of 1s

b. Theorem

Let B = {1^ky|y∈{0,1}* and y contains at most k 1s, for k ≥ 1}. Show that B is not a regular language.

b. Proof

As shown in 1.77 Sipser's example, we can apply an absurd proof of the pumping lemma to this language

Let we assume that B is regular. Let we choose one 1 as pumping's y and the second part (i.e. from the first 0 found) as pumping's z, and it seems to work:

$\underset{y}{\underbrace{1111}}\underset{z}{\underbrace{0100}}$

or better

$\underset{y_1}{\underbrace{1}}\underset{y_2}{\underbrace{1}}\underset{y_3}{\underbrace{1}}\underset{y_{\mathrm{n}}}{\underbrace{1}}\underset{z}{\underbrace{0100}}$

Pumping lemma doesn't allows a length of 0 for the y part, but allows that y is repeated zero times.

Using as example the previous string, with y repeated zero times, we obtain the string 0100, that doesn't match. Thus we obtain a contradiction.