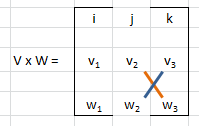Schema sintetico per la risoluzione delle equazioni differenziali
Prospetto
- Variabili separabili → integrazione per y a destra e per x a sinistra
- Primo ordine →
- Secondo ordine
- Omogenea
- Δ > 0 → C1eλ1x+C2eλ2x
- Δ = 0 → C1eλ1x+xC2eλ2x
- Δ < 0 → eαx(C1cos(βx)+C2sin(βx))
- Non omogenea (come la omogenea più:)
- Senza funzioni trigonometriche, con α soluzione → xmp(x)eαx
- Senza fx. trig., senza α soluzione → p(x)eαx
- Con fx. trig., con α soluzione → xeαx(P(x)cos(βx)+Q(x)sin(βx))
- Con fx. trig., senza α soluzione → eαx(P(x)cos(βx)+Q(x)sin(βx))
- Omogenea
Algebra lineare - l'inizio
Sarò strano, ma non mi semrba che i primi paragrafi di AL siano particolarmente difficili.
Campo
Un campo è una quintupla(1) (X, +, -, ·, 0, -1, 1) dove X è un insieme, + e · sono operazioni binarie, -, -1 sono operazioni unarie e 0, 1 costanti che soddisfano le seguenti equazioni.
- Proprietà associativa: x+(y+z) = (x+y)+x e x·(y·z) = (x·y)·z
- Proprietà commutativa: x+y = y+x e x·y = y·x
- Elementi neutri: x+0 = x e x·1 = x
- Proprietà distributiva: x·(y+z) = x·y + x·z
- Opposto: x+(-x) = 0
- Inverso: x·x-1 = 1
- Prodotto per zero: x·0 = 0
Sono sempre i soliti concetti!
ℕ non è un campo, perché non vale l'opposto né l'inverso, fatta eccezione per 1. Se poi si considera ℕ ∩ 0 = ∅, allora non c'è l'elemento neutro per la somma né il prodotto per zero.
ℤ ha qualcosa in più ma non è ancora un campo.
ℚ è un campo.
ℝ è un campo, ma i soli irrazionali ℝ\ℚ no, poiché, per esempio π / π = 1, che è razionale.
Spazio vettoriale
I vettori possono essere un vero casino, a meno di non tenere a mente un paragone con un'applicazione pratica delle definizioni.
Il vettore si può immaginare come una forza applicata a un oggetto. Per esempio, un cavallo che traina un carretto è una buona metafora per un vettore (la forza che esercita il cavallo per trainare il carretto), per la direzione del vettore (la direzione verso cui il cavallo tira) e per l'applicazione del vettore (il "punto di partenza" del vettore è il carretto).
Uno scalare si può immaginare come uno "zoom" avanti o indietro. Se vado avanti, vedo il vettore più grande, indietro più piccolo. Lo scalare non cambia la direzione.
In generale, un vettore può essere rappresentato da una serie di numeri. Se osservo dall'alto il famoso cavallo, posso rappresentare il vettore in uno spazio bidimensionale, e dire, per esempio "il cavallo traina il carretto verso nord-ovest con una forza 2,3 N". Se osservo due uccelli contendersi un pezzo di pane, non sono più sufficienti due dimensioni, perché potrebbero esercitare sul pane una forza verso nord-sud, est-ovest ma anche alto-basso.
Somme di vettori
Per sommare due vettori immaginiamo due scenari semplici. Un carretto, stavolta trainato da due cavalli, che tirano nella stessa direzione con la stessa forza, per esempio 2,3 N.
Trainando nella stessa direzione, la forza esercitata è 2,3 N + 2,3 N = 4,6 N.
Se trainassero invece in direzione opposta, la forza sarebbe 2,3 N - 2,3 N = 0. In pratica, il carretto starebbe fermo.
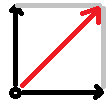
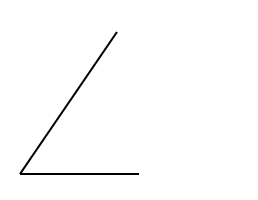
E se invece trainassero uno verso nord e l'altro verso est?
Il risultato è che andrebbero verso nord-est, come è intuibile, ma con che forza?
Come si vede dal disegno (pietà, è fatto con paint!) la forza sarebbe maggiore del singolo vettore, ma minore della somma. In questo caso particolare, siccome la forza con cui i cavalli trainano è esattamente a 90° ed è esattamente uguale, si può applicare il teorema di Pitagora in questa maniera:
Siccome abbiamo disegnato un quadrato, e la diagonale di un quadrato di lato 1 è circa 1,41, sarebbe bastato anche moltiplicare per √2 il numero 2,3.
Per identificare il punto "finale" del vettore risultante (quello in rosso, nel disegno), basta sommare una a una le dimensioni del primo e del secondo vettore.
Per esempio, il primo (orizzontale) potrebbe iniziare in P0 = (5, 4) e finire in P1 = (7.3, 4), mentre il secondo inizia sempre in P0 = (5, 4) e termina in P1 = (5, 6.3). Il vettore risultante inizia quindi in P0 = (5, 4) e finisce in P1 = ((5 + (7.3-5)), 4 + (6.3-4)) e quindi in P1 = (7.3, 6.3).
Possiamo capire quindi che il punto iniziale potrebbe non essere P0 = (0, 0), ma un punto qualunque. I calcoli diventano un po' più complicati ma il risultato non cambia.
Per sapere la lunghezza del vettore, basta "togliere" la base, cioè "normalizzare" il vettore in P0 = (0, 0) e applicare il teorema di Pitagora.
Prodotto vettoriale
Con il prodotto vettoriale finalmente le cose si complicano un po'.
Il prodotto tra due vettori restituisce un terzo vettore perpendicolare agli altri due. Come è possibile?
Perché due vettori (con direzioni diverse) definiscono un piano, quindi un vettore perpendicolare al piano è perpendicolare anche ai due vettori.
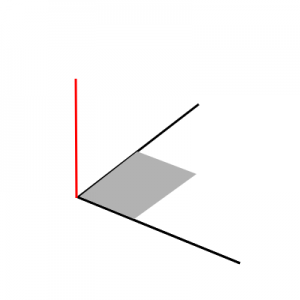
La cosa poco intuitiva è che mentre i due vettori definiscono uno spazio ℝ2 - cioè uno spazio in cui ogni punto corrisponde a una coppia di numeri reali - il vettore risultante va in una terza direzione e "usa" solo quella.
Un'altra cosa poco intuitiva è che il prodotto vettoriale definisce una superficie pari all'area del parallelogramma definito dai due vettori:
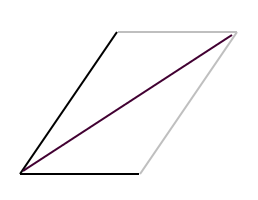

L'aspetto un po' destabilizzante è che dal punto di vista fisico, la superficie del parallelogramma corrisponde a una lunghezza e che questa lunghezza ha una direzione perpendicolare al piano su cui giacciono i due vettori.
Un approccio matematico
Per calcolare questa area è possibile usare lo strumento del calcolo a matrice in questo modo.
Chiamiamo i due vettori da moltiplicare V = (V1, V2, V3) e W = (W1, W2, W3) e il vettore risultante R = (i, j, k).
Nel paragrafo precedente parlavo di un piano, e il piano più semplice da immaginare è quello in cui la coordinata "z" (nei disegni, quella che identifica alto/basso) è immaginata sempre a zero. In realtà i due vettori potrebbero essere su un piano inclinato rispetto al sistema di riferimento, ed è per questo che devono essere identificati da tre coordinate e non due.
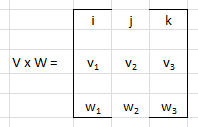
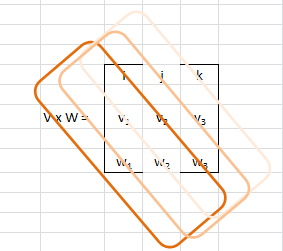
Nel caso di una matrice di dimensione 3x3, il prodotto vettoriale si può scrivere in questo modo (regola di Sarrus):
Si sommano le diagonali alto-sinistra <--> basso destra, come questa:
i·v2·w3
aggiungiamo le altre tre diagonali:
i·v2·w3 + j·v3·w1 + k·v2·w3
e poi togliamo le altre tre diagonali:
i·v2·w3 + j·v3·w1 + k·v2·w3 - i·v3·w2 + j·v1·w3 + k·v2·w1
a questo punto si possono raccogliere i, j e k:
i·(v2·w3-v3·w2) + j·(v3·w1-v1·w3) + k·(v1·w2-v2·w1)
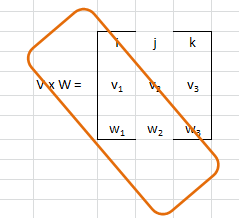
graficamente, così si calcola i (arancione si somma, celeste si sottrae):
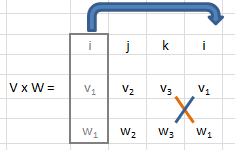
Per calcolare j è sufficiente spostare i a destra:
Omologo per k.
Esempio di prodotto di vettori
V = (1, 2, 3)
W = (1, 0, 1)
R = (2x1 - 3x0, 3x1 - 1x1, 1x0 - 2x1) = (2, 2, -2)
Di seguito un banale excel che esegue i calcoli per noi:
Prodotto vettoriale
Studio di una funzione: log(x^2+5x-6)
Funzione tratta da http://matepratica.tutorando.com
Teorema master sulle ricorrenze
Siano a ≤ 1 e b ≤ 1 costanti e f(n) una funzione.
Sia T(n) il costo dell'esecuzione della ricorrenza.
Keep reading →
Visite di alberi
Oggi ho scoperto l'acqua calda.
Dopo settimane passate a cercare di memorizzare l'ordine delle visite degli alberi ho realizzato questi grafici sul mio Display a Fibre di Cellulosa™
Keep reading →
Dimostrazione che n^2 >= 2n + 5
Dimostrare per induzione che n2 ≥ 2n + 5 ∀ n ≥ 4
Base: 42 ≥ 2·4 + 5 ⇒ 16 ≥ 13: verificato
Passo induttivo: n2 ≥ 2n + 5 ⇒ (n+1)2 ≥ 2(n+1) + 5
(n+1)2 = n2 + 2n + 1
per ipotesi induttiva (l'ipotesi è n2 ≥ 2n + 5) possiamo dire che
n2 + 2n + 1 ≥ 2n + 5 + 2n + 1
2n + 5 + 2n + 1 = 2n + 2 + 2n + 4 = 2(n+1) + 2(n+2)
il passo induttivo è dimostrato se 2(n+1) + 2(n+2) ≥ 2(n+1) + 5 ⇒ 2n+4 ≥ 5 ⇒ 2n ≥ 5-4 che è vero ∀ n ≥ 4 ∎
Riflessioni di preparazione per il compito di Matematica Discreta
Premessa. Qualche mese fa mi sono preso un bidone: mi ero iscritto all'anno accademico 2014-2015, ma a causa dei crediti riconosciuti dalla carriera precedente mi sono ritrovato iscritto con l'ordinamento 2013-2014.
"amen - ho pensato - tanto le materie saranno sempre le stesse". E invece, mi sono ritrovato con Calcolo 1 e Calcolo 2 trasformati in Calcolo e basta (12 crediti) e Matematica Discreta + Algebra lineare trasformati in Matematica Discreta (12 crediti).
Keep reading →
Elenco degli algoritmi di ordinamento
La seguente tabella riepiloga gli algoritmi di ordinamento.
La spiegazione del funzionamento è solo un promemoria, non ha intento di essere esauriente.
| Algoritmo | Complessità | Funzionamento |
|---|---|---|
| InsertionSort | O(n2) | (base) Si lascia il primo elemento dov'è
(passo induttivo) Per ogni elemento n, si trova il primo elemento maggiore tra quelli già ordinati, si sposta di una posizione da lì a n e si inserisce n tra quello appena minore e quello appena maggiore |
| SelectionSort | O(n2) | (base) Si scorre l'elenco trovando quello più piccolo e si scambia con il primo.
(passo induttivo) Posto che fino all'elemento n-1 l'elenco è ordinato e contiene solo elementi più piccoli di quelli ancora da ordinare, si scorre l'elenco da n alla fine e si scambiano l'n-esimo con il più piccolo. |
| BubbleSort | O(n2) | (base) Si confrontano il primo e il secondo elemento. Se il primo è minore del secondo non si fa niente, se il secondo è minore del primo si scambiano.
(passo induttivo) Si scorre tutto l'insieme effettuando scambi a coppie se il primo elemento è maggiore del secondo. Si procede finché tutto l'elenco non è ordinato. In pratica, si identifica al termine del primo ciclo l'elemeno più grande, poi il vice-più grande e così via |
| HeapSort | O(nlog(n)) | Utilizzando un heap si trasferisce la lista nell'heap e poi si rimuovono uno a uno gli elementi. Se max-heap si rimuove il più grande e si mette alla fine, se min-heap il contrario. |
| MergeSort | Θ(nlog(n)) | Algoritmo divide-et-impera (Impera) avendo due sequenze ordinate da fondere, basta estrarre di volta in volta l'elemento più piccolo tra i due elementi correnti delle due code e incrementare l'indice. (Divide) divide l'array in due parti uguali e applica il mergesort stesso a entrambe le metà. |
| QuickSort | O(n2) (caso peggiore), O(nlog(n)) (caso medio) | Algoritmo divide-et-impera (Impera) concatena i due pezzi di array divisi dalla parte divide. (Divide) divide l'array in due parti, in cui la prima contiene gli elementi ≥ x e la seconda gli elementi < x, dove x è un numero scelto casualmente. |
| IntegerSort
Nota: è detto anche CountingSort |
O(n+k), dove k è l'intero più grande dell'array | L'algoritmo usa un array A di appoggio di dimensione k, in cui a ogni elemento e dell'array di partenza incrementa A[e]. Alla fine scorre l'array A aggiungendo un elemento a ogni A[i] > 0 e decrementa A[i]. |
| BucketSort | O(n+k), dove k è l'intero più grande dell'array | L'algoritmo funziona in maniera molto simile a IntegerSort, ma ordina record invece che interi e quindi non può usare solo un array di interi ma deve usare una lista di record. |