Gennaio 2019 Archive

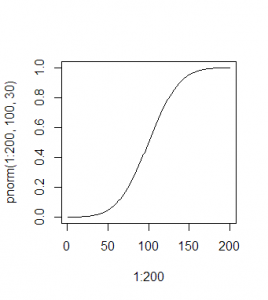
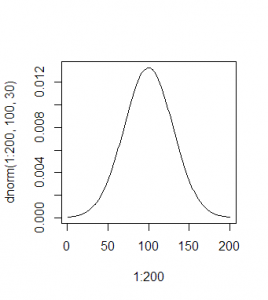
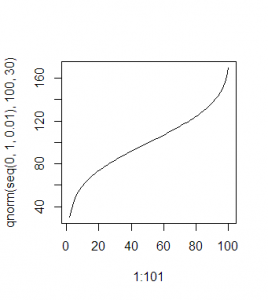
La distribuzione ipergeometrica mostra la distribuzione di n estrazioni da un campione di tipo bianco/nero (solo due scelte chiaramente distinte) senza reinserimento.

I parametri sono:

1. x/q/p/nn: uno o più valori richiesti
2. w: il numero di casi di successo (palline bianche nell'urna)
3. b: il numero di casi di non successo (palline nere nell'urna)
4. n: il numero di estrazioni

Nell'esempio di 17 studenti maschi, considerati "successo" nell'esempio, e 13 studentesse (totale: 30 studenti), per sapere la probabilità di ottenere esattamente 2 maschi su 3 estrazioni, si utilizza:

> dhyper(2, 17, 13, 3)
[1] 0.435468

In R le distribuzioni riportano un prefisso che può essere una lettera tra p, q, d, r.

• p significa "probabilità" della distribuzione
• q significa "quantile"
• d significa "densità"
• r significa "randon", cioè valore casuale

Gli esempi seguenti si basano sulla distribuzione normale con μ=100 e σ=30 da 1 a 200.

pnorm rappresenta la funzione di ripartizione, che - come previsto - inizia a zero e tende a 1; dnorm rappresenta la probabilità e disegnando la probabilità di ciascun punto da 1 a 200 si ottiene la classica gaussiana:

qnorm rappresenta il valore che si trova al quantile, quindi il primo parametro che prende è un valore da 0 a 1. Per esempio, la mediana si ottiene passando come primo parametro 0.5:

> qnorm(0.5, 100, 30)
[1] 100

Volendo rappresentare con un grafico l'andamento dei quartili si può utilizzare la funzione qnorm(seq(0, 1, 0.01), 100, 30), che produce questo grafico:

rnorm restituisce una certa quantità (primo parametro) di valori casuali con la distribuzione scelta.