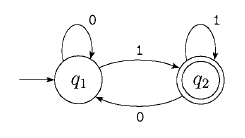
Pushdown automata
Un pushdown automata è descritto come un insieme di stati Q, un alfabeto di input Σ, un alfabeto di stack Γ, un insieme di funzioni δ QxΣεxΓε → QxΓε, uno stato di partenza e un insieme di stati accettati. All'inizio lo stato è quello iniziale q0 e lo stack è vuoto.
Nei diagrammi gli stati sono rappresentati dai "soliti" pallini con gli identificativi di stato qqualcosa, mentre le frecce sono etichettate con σ, γ1 → γ2, dove γ1 e γ2 sono elementi dell'alfabeto dello stack Γ. Questo va interpretato come: se l'input è σ, allora leggo γ1 e scrivo γ2. Formalmente γ1 e γ2 sono sempre presenti, ma se il valore è ε allora effettuo il passaggio senza leggere o scrivere niente.
Quando devo dimostrare che un linguaggio riconosciuto da un pushdown automata è equivalente a un linguaggio context-free, inizio dicendo che se un linguaggio è context-free allora un pushdown automata lo riconosce.
Un CLF funziona sostituendo di volta in volta stringhe con altre stringhe più grandi, quindi il problma principale sta nel memorizzare questa stringa in un PDA. Per fare questo, si scrive la stringa nello stack. Ma lo stack può leggere o scrivere solo un carattere alla volta.
La funzione di transizione ha la caratteristica di essere nella forma δ(q, a, x) = (r, y), dove:
- q è lo stato attuale
- a è il carattere di Σ di input
- x è il carattere di Γ letto dalla pila
- r è lo stato di destinazione
- y è il carattere di Γ scritto nella pila
La funzione di transizione deve essere una tra le seguenti:
- δ(q, a, x)
- δ(q, ε, x)
- δ(q, a, ε)
- δ(q, ε, ε)
in altre parole, lo stato di partenza è - ovviamente - necessario, ma non è necessario che ci siano né un carattere di input (come negli NFA) né un carattere di stack.