Funzioni efficienti (grafi) 27/05/2017
Il seguente algoritmo accetta in ingresso la matrice di adiacenza di un grafo non orientato e restituisce un valore Booleano (TRUE / FALSE)
MyAlgorithm( A ) 1. n = rows(A) /* determina il numero di vertici del grafo */ 2. let B an n x n matrix /* alloca memoria per una matrice B n x n */ 3. for i = 1 to n 4. for j = 1 to n 5. b[i,j] = 0 6. for k = 1 to n 7. b[i,j] = b[i,j] + a[i,k]*a[k,j] 8. for i = 1 to n 10. for j = i + 1 to n 11. if a[i,j]*b[i,j] <> 0 then 12. return FALSE 13.return TRUE
Si calcoli la complessità computazionale di MyAlgorithm e si determini la sua funzione (in quali casi restituisce TRUE? in quali casi FALSE?). (Nota: Nel determinare la complessità si ignori per comodità la complessità delle istruzioni 1 e 2).
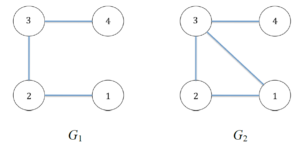
Si simuli inoltre il suo comportamento sui seguenti due grafi, verificando che restituisca il risultato atteso:
Risposta
L'algoritmo è trattato nella lezione 10 di Pelillo, in cui si parla del risultato di un prodotto tra la matrice di adiacenza e se stessa, e dei successivi prodotti tra la matrice e il risultato precedente.
Una volta terminato la prima serie di cicli annidati, di costo O(n3), si verifica con un'altra serie di cicli annidati, di costo O(n2), se esistono archi in comune. Se esistono (confronto alla riga 11), il grafo ha almeno un ciclo di lunghezza 3 vertici.
Il costo complessivo è O(n3) + O(n2), quindi O(n3).
Il comportamento si basa su matrice di adiacenza e matrice di appoggio.
Le matrici di adiacenza sono:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | 0 |
| 2 | 1 | 0 | 1 | 0 |
| 3 | 0 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 | 0 |
e per il secondo grafo
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 |
| 3 | 1 | 1 | 0 | 1 |
| 4 | 0 | 0 | 1 | 0 |
Una volta terminati le 64 esecuzioni (4 x 4 x 4) della riga 7, si ottengono le seguenti matrici:
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 |
| 2 | 0 | 2 | 0 | 1 |
| 3 | 1 | 0 | 2 | 0 |
| 4 | 0 | 1 | 0 | 1 |
Questa matrice è "complementare" a quella del primo grafo, che infatti non presenta cicli.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 1 |
| 3 | 1 | 1 | 2 | 0 |
| 4 | 1 | 1 | 0 | 1 |
Questa seconda matrice ha in comune con la seconda matrice di adiacenza i tre archi ((1, 2), (2, 3), (3, 1)) che costituiscono il ciclo.