Dopo aver scritto un piccolo riepilogo sulle parabole e la corrispondenza tra grafico e termini dell'equazione, facciamo qualche considerazione sul significato di vertice.
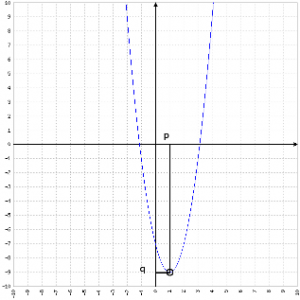
Definiamo il vertice della parabola V=(p,q) e definiamo a, b, c, nella maniera "classica" i fattori che moltiplicano rispettivamente x2, x1 (cioè x), x0 (quindi c è costante): in pratica l'equazione della parabola è ax2+bx+c.
Table of Contents
X del vertice
Appare evidente che il termine costante "alza" e "abbassa" la parabola, quindi non influisce in alcun modo nel determinare lo spostamento "orizzontale" (p, sull'asse x).
Lo spostamento orizzontale dipende da quanto "larga" è la parabola (più cresce a, più stretta è la parabola) e quanto "scivola" a destra o sinistra (più cresce b, più la parabola scivola a sinistra se a>0 o destra se a<0).
In che rapporto sono la crescita di a, che stringe la parabola e la fa tendere verso il centro, e b, che la trasla anche in orizzontale?
A ogni traslazione di un'unità di b corrisponde uno spostamento determinato da metà di a.
Quindi, per fare un paio di esempi:
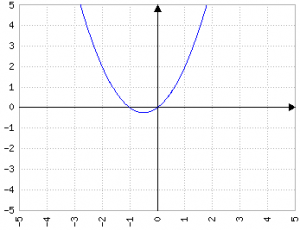
| Valore di n | Valore di p |
|---|---|
| 0 | 0 (passa per (0,0)) |
| 1 | -1/2 |
| 2 | -1 |
| 3 | -3/2 |
| 1000 | -500 |
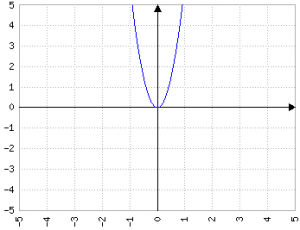
| Valore di n | Valore di p |
|---|---|
| 0 | 0 (passa per (0,0)) |
| 1 | -1/6 |
| 2 | -1/3 |
| 6 | -1 |
| 600 | -100 |
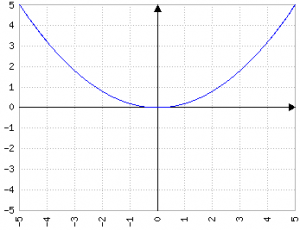
| Valore di n | Valore di p |
|---|---|
| 0 | 0 (passa per (0,0)) |
| -1 | 1/4 |
| -2 | 1/2 |
| -4 | 1 |
| -1000 | 250 |
Dato che aumentare o diminuire a fa diminuire o aumentare l'"influenza" di b sia a sinistra sia a destra, a va raddoppiato.
La formula per ottenere p è quindi:
Significato di Δ
Il delta (Δ) di una parabola rappresenta la "distanza" nell'asse x tra le due soluzioni, ed è dato da
Come già detto precedentemente, Δ > 0 significa che la parabola interseca l'ascissa due volte ("andata" e "ritorno"); Δ = 0 significa che la parabola tange l'ascissa, e quindi la tocca una volta sola; Δ < 0 significa che la parabola non interseca l'ascissa.
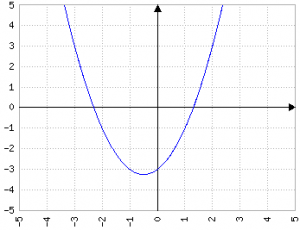
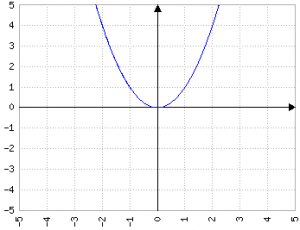
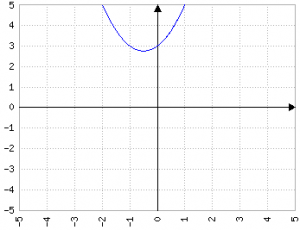
È evidente che aumentare o diminuire a quando b=0 e c=0 non cambia minimamente il valore di Δ, perché le modifiche alla parabola non coinvolgono il vertice (0,0).
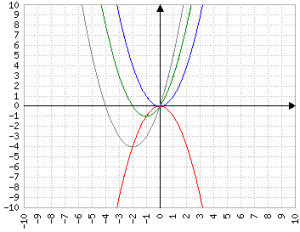
Il termine b è molto importante, perché (con a>0) fa "scivolare" la parabola in basso (e a sinistra) lungo una parabola di segno invertito.
Dal momento che b "agisce" sul discriminante lungo una parabola, il suo valore va considerato elevato al quadrato, e dal momento che fa "scendere" la parabola, ne va preso il valore negativo -b^2 (nel disegno è la parabola rossa):
Il termine c "alza" la parabola, quindi agisce in maniera contraria rispetto a b.
Ovviamente il termine b dipende in maniera forte dal valore di a (con b≠0, a torna ad essere importante):
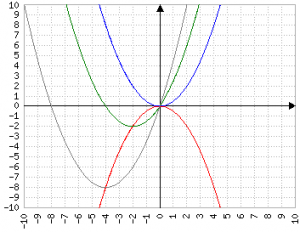
Il valore di a (all'aumentare "stringe" la parabola) diminuisce l'importanza di b.
Abbiamo dunque un termine b che vale per il suo quadrato, da un lato; dall'altro abbiamo a e c che "contrastano" il valore di b per un fattore 4.
(completare)
Y del vertice
(completare)