23
Questa è stata la medaglia più sudata.
Partito con la terza media e vent'anni di totale assenza di matematica, ho passato il primo anno a studiare il programma delle superiori e limiti+derivate.
Non ho superato il primo appello (per chi mi chiama secchione...), ma sapevo da prima che non ero abbastanza preparato. Allora ho preso in mano un libro delle superiori e ho fatto (quasi) tutti gli esercizi. Poi alla fine ho ripreso in mano limiti e derivate.
Ho affrontato il secondo appello senza sapere gli integrali per sostituzione, ma nell'esame ho trovato un banale
cioè l'esercizio uno degli integrali per party.
Quando ho affrontato analisi II ho capito che non solo dovevo imparare gli integrali per sostituzione, ma anche Ruffini, la scomposizione in fratti semplici, i numeri complessi, le equazioni differenziali (con tutte le varianti), gradiente e matrice hessiana, integrazione a due variabili, cambio in coordinate polari e una buona dose di "furbate" che impari solo con l'esercizio.
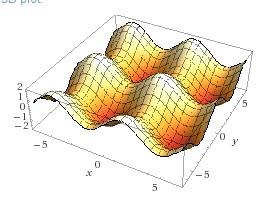
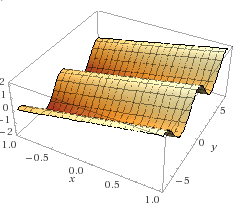
L'unico aspetto confortante è la mia abilità nel riconoscere nelle equazioni le forme fisiche, per es. z = sin(x) + cos(y) è la scatola delle uova, z = x + cos(y) è la tettoia
che mi ha portato per un periodo a vedere in un lenzuolo tenuto con le mani una funzione a due tre variabili :-O
Ora posso dimenticarmi tutto 😉
Mio figlio (seconda elementare) in un anno ha affrontato le quattro operazioni. Qualche giorno fa mi diceva:
sei più sette fa... tredici
cinque per tre fa... quindici
due meno tre fa...
...
facciamo sette meno due... cinque
dodici diviso tre fa... quattro
tredici diviso quattro fa...
...
facciamo diciassette diviso uno... diciassette!
Buona fortuna, piccolino.