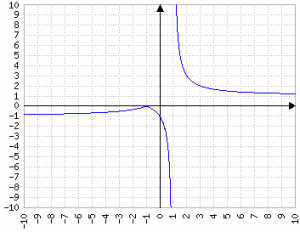
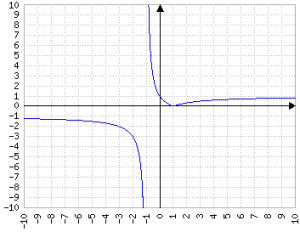
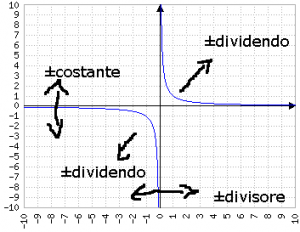
Regola generale: se il divisore e il dividendo sono uguali, il risultato è un valore costante 1 con dominio ℝ\{0} (per tutta la trattazione si esclude implicitamente o esplicitamente quandi il divisore è zero)
Se sono diversi, appare un'iperbole (magari "distorta"), nei quadranti 1, 3 se la frazione ha segno positivo, nei quadranti 2, 4 se ha segno negativo.
| Dividendo | ||||
|---|---|---|---|---|
| Cost. | 1° | 2° | ||
| Divisore | Cost. | |||
| 1° | ||||
| 2° | ||||
Table of Contents
Costante sopra, costante sotto
Banale divisione, con un risultato costante.
Variabile di primo grado sopra, costante sotto
È una versione senza q dell'equazione della retta y=mx+q, anche qui niente di speciale.
La presenza di una costante, se ≠ 0, garantisce che la funzione abbia valore sempre, in quanto non è mai presente una divisione per zero.
Costante sopra, Variabile di primo grado sotto
Già discusso qui: appunti-di-calcolo-funzioni-razionali
Riassumendo:
Costante sopra, Variabile di secondo grado sotto
In questo caso è molto utile conoscere il Δ: se è < 0 significa che il divisore non vale mai zero, e quindi il grafico è una "cunetta" che non schizza mai all'infinito.
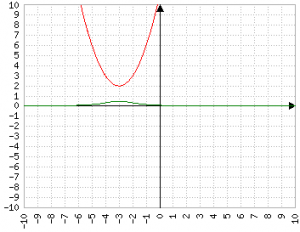
Se Δ è uguale a zero c'è un solo punto in cui la parabola ha valore zero e quindi c'è un solo punto in cui 1/f(x) tende a +∞. Essendo una funzione di secondo grado con Δ ≤ 0, il grafico non è mai negativo.
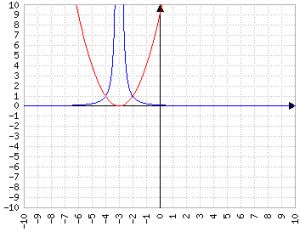
Se Δ è > zero, per i punti esterni alle soluzioni il valore è positivo, per i punti interni è negativo e in corrispondenza delle soluzioni ci sono due limiti che esternamente tendono a +∞ e internamente a -∞
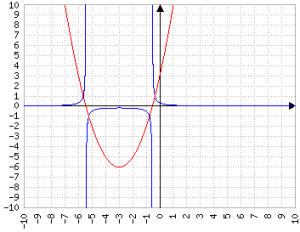
Variabile di secondo grado sopra, costante sotto
Nessuna sorpresa particolare: la parabola si "allarga". Un effetto simile si ottiene abbassando il primo termine (ax2).
Variabile di primo grado sopra, Variabile di primo grado sotto
Due casi: il caso generico, in cui divisore e dividendo si intersecano fuori da y=0, si ha sempre un'iperbole, come scritto sopra, nei quadranti 1-3 oppure 2-4, a seconda del segno.
Nel caso in cui dividendo (f(x)) e divisore (g(x)) si intersechino in y=0, il risultato è una costante data da f(x)/g(x) per qualunque x, tranne il caso in cui il g(x) = f(x) = 0. Questo punto (f(x)/g(x), 0) è esterno al dominio.
Per es, con
il dominio è ℝ\{2}
Variabile di secondo grado sopra, Variabile di secondo grado sotto
Si crea una "doppia iperbole", con asintoti nelle soluzioni dell'equazione di secondo grado.
Attenzione! Se una delle due soluzioni è 0/0 (zero su zero), uno degli asintoti MANCA completamente (ovviamente il punto che da come risultato 0/0 è esterno al dominio):
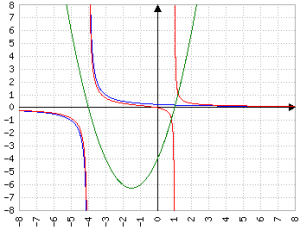
In blu il dividendo è x-1 e in rosso il dividendo è x
Valore assoluto sopra
Se l'equazione è diversa da |x|/x, le soluzioni dell'equazione sono composte da tre insiemi: quando il dividendo e il divisore sono < 0, quando sono entrambi > 0 e quando il loro segno è discorde.
Quando sono entrambe < 0, siccome sopra c'è un valore assoluto e sotto un valore negativo, le soluzioni sono negative.
Quando sono entrambe > 0, le soluzioni sono positive.
Quando le soluzioni sono diverse, a seconda di qual è il termine maggiore ci può essere un brusco cambio di direzione in un ramo o nell'altro: