2. Riepilogo generale / 2

Equazioni e disequazioni con modulo

Le soluzioni di un'equazione con modulo sono, per
f:A→ℝ
|f(x)|=k

k < 0 ↠ impossibile
k = 0 ↠ f(x) = 0
k > 0 ↠ |f(x)|-k = 0

Esempio

f:A→ℝ
f(x)=|x^2-5| = 1

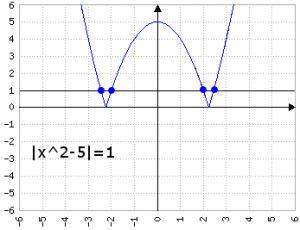
Il segno (positivo dentro il valore assoluto) indica che la parabola è rivolta verso l'alto; il Δ = +20 indica che esistono due soluzioni; però il valore assoluto fa raddoppiare ulteriormente le soluzioni, che diventano quattro perché il termine dopo l'uguale è ≠ 0.

Disequazioni

Le soluzioni delle disequazioni è "interna" al valore assoluto se la disequazione ha segno minore, "esterna" con segno maggiore.

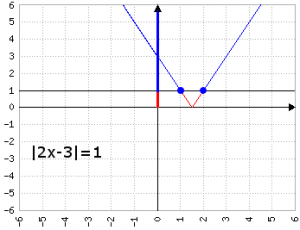
Nel grafico della funzione di esempio, la disequazione ha come soluzioni:

$\left\{\begin{array}{}\le \Rightarrow -1\le 2x-3\le 1\\ \ge \Rightarrow 2x-3\le -1\bigcup 2x-3\ge 1\end{array}\right.$

Equazioni e disequazioni razionali

Esempio

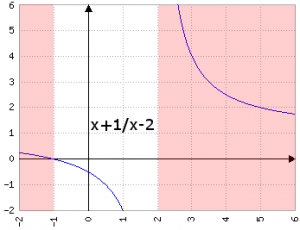
f:ℝ\{2}→ℝ

$\left|\frac{x+1}{x-2}\right|\ge 5$

 

I passaggi per la soluzione sono:

$\left|\frac{x+1}{x-2}\right|\ge 5$

Determino il segno:

	-1		2
$x+1$	-	+		+
$x-2$	-	-		+
Segno	+	-		+

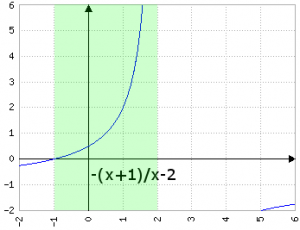
devo risolvere per

$\frac{x+1}{x-2}\ge 5$

con dominio (-∞, -1] ⋃ (2, +∞) e anche per

$-\left(\frac{x+1}{x-2}\right)\ge 5$

con dominio [-1, 2)

Nota: nel punto (-1, 0) è indifferente considerare un caso o l'altro, perché in entrambi i casi x+1=0. Viceversa x=2 è escluso in partenza da entrambi i domini.

---

Alla fine, quindi, x è compreso tra 3/2 e 11/4, escluso 2, poiché l'abbiamo escluso dal dominio dall'inizio.

$x\in \left[\frac{3}{2},\frac{11}{4}\right]\backslash \left\{2\right\}$

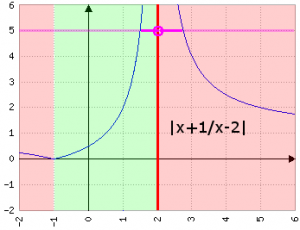
Equazioni di secondo grado

Le equazioni di secondo grado, solitamente rappresentate da

$a{x}^2+bx+c$

oppure da

$a_0+a_{1}x+a_2{x}^2$

possono essere rappresentate in forma semplificata come equazione basata sul vertice della parabola (p,q) nella maniera seguente, se il moltiplicatore dell'incognita di grado 2 è 1 (in pratica, la parabola non è "stretta" o "larga"):

$y={\left(x-p\right)}^2+q$

-q corrisponde di fatto al discriminante, poiché con -q<0 non ci sono soluzioni con -q c'è una sola soluzione x passante per l'asse e>0 ci sono due soluzioni (cioè il vertice è < 0): ±√(q)+p

Equazione con vertice e molt. incognita di grado 2 ≠ 1

Radicali

Le radici si comportano in maniera differente se l'esponente è pari o dispari.
Nel primo caso la base DEVE essere positiva, in quanto (in ℝ) non esiste alcun numero che elevato a una potenza pari dia -1 come risultato.
Nel secondo caso la base può essere positiva o negativa, nel qual caso il risultato sarà negativo.

Basi ed esponenti

	Esponente PARI	Esponente DISPARI
Base POS o zero	Risultato ± n	Risultato ≥ 0
Base NEG	Non possibile	Risultato < 0

Mettere a fattor comune radici diverse

Basta mettere sotto radice MCM tra le due radici. Esempio:

$\sqrt[3]{f\left(x\right)}=\sqrt[4]{g\left(x\right)}$

---

$\sqrt[12]{{f\left(x\right)}^4}=\sqrt[12]{{g\left(x\right)}^3}$

---

${f\left(x\right)}^4={g\left(x\right)}^3$

Altro esempio:

$\sqrt[3]{x^3+2}-1=x$

---

Passo -1 dall'altro lato

$\sqrt[3]{x^3+2}=x+1$

---

Elevo tutto alla terza

${\left(\sqrt[3]{x^3+2}\right)}^3={\left(x+1\right)}^3$

---

Semplifico il primo termine

$x^3+2={\left(x+1\right)}^3$

Altro esempio:

$\sqrt{2x-1}=x-1$

---

Il primo termine deve dare un risultato positivo, quindi x-1≥0, cioè x≥1.
Il termine sotto radice deve essere positivo, quindi 2x-1≥0, quindi x≥1/2.
Sviluppo l'uguaglianza:

$2x-1={\left(x-1\right)}^2$

---

$2x-1=x^2-2x+1$

---

$x^2-2x-2x+1+1=0$

---

$x^2-4x+2=0$

---

$\mathrm{soluzioni}=\frac{4\pm \sqrt{16-8}}{2}=2\pm \sqrt{2}$

---

Ma siccome 2-√2 < 1, l'unica soluzione nel codominio è 2+√2.

---

Altro esempio: elevare alla n-esima potenza:

$\sqrt[n]{f\left(x\right)}=g\left(x\right)$

---

Se n è dispari, posso elevare tutto alla n e via:

$f\left(x\right)={\left(g\left(x\right)\right)}^{\mathrm{n}}$

---

Se n è pari, prima di elevare tutto alla n devo porre:

$\left\{\begin{array}{c}f\left(x\right)\ge 0\\ g\left(x\right)\ge 0\end{array}\right.$

e poi elevo:

$f\left(x\right)={\left(g\left(x\right)\right)}^{\mathrm{n}}$

---

Disequazioni con radici:

$f\left(x\right)>\sqrt[n]{g\left(x\right)}$

---

Se n è pari, devo porre entrambe le funzioni ≥ 0, poiché né il radicando né il risultato di una radice pari possono essere negativi; in ogni caso pongo:

$f\left(x\right)>g\left(x\right)$

---

Cambio di verso:

$f\left(x\right)<\sqrt[n]{g\left(x\right)}$

---

Se n è pari, devo porre:

$\left\{\begin{array}{c}f\left(x\right)<0\\ g\left(x\right)\ge 0\end{array}\right.\bigcup \left\{\begin{array}{c}f\left(x\right)>0\\ {f\left(x\right)}^n\le g\left(x\right)\end{array}\right.$

La seconda implica automaticamente che g(x) sia > 0.

---

Risolviamo questo:

$\left(x-1\right)>\sqrt{5-2x}$

Poniamo subito le condizioni di esistenza:

$\left\{\begin{array}{cc}\mathrm{(1)}& 5-2x\ge 0\Rightarrow x\le \frac{5}{2}\\ \mathrm{(2)}& x-1>0\Rightarrow x>1\end{array}\right.$

---

Con le dovute premesse possiamo elevare:

${\left(x-1\right)}^2>5-2x$

---

...e sviluppare:

$x^2\sout{-2}x+1>5\sout{-2x}$

---

$x^2-4>0$

---

$\left(x-2\right)\left(x+2\right)>0$

---

Otteniamo (3) x<-2 ⋃ (4) x>2, ma per (1) dobbiamo escludere il risultato negativo. Inoltre (4) comprende (1), quindi le condizioni da soddisfare sono:

• x>1, perché altrimenti la radice del secondo termine dovrebbe essere negativa
• x>2, perché con x≤2 la disequazione non sarebbe soddisfatta
• x≤5/2, perché con un x più grande ci sarebbe un numero negativo sotto radice

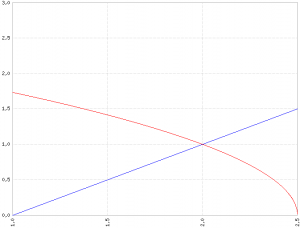
Si può verificare graficamente il significato delle tre proposizioni qui:

zoom:

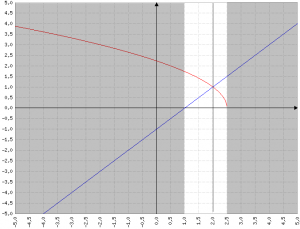
Il risultato quindi è che la disequazione è soddisfatta nell'intervallo (2, 2.5]

---

Esercizio: risolvere:

$x-1<\sqrt{x+3}$

---

Condizioni di esistenza:

$\left\{\begin{array}{c}x+3\ge 0\Rightarrow x\ge -3\\ x-1<0\Rightarrow x<1\end{array}\right.\bigcup \left\{\begin{array}{c}x-1\ge 0\Rightarrow x\ge 1\\ {\left(x,-,1\right)}^2<x+3\Rightarrow x^2-2x+1<x+3\Rightarrow x^2-3x-2<0\end{array}\right.$

Sviluppando l'ultima disequazione di II grado:

$\frac{3\pm \sqrt{9+8}}{2}$

---

Il risultato quindi:

• Non esiste al di sotto di -3 (per -3 invece esiste)
• È vero per l'intervallo [-3,+1]⋃[(-3-√17)/2, (-3+√17)/2), ma siccome +1<(-3-√17)/2 possiamo dire che è vero per [-3, (-3+√17)/2)
• È falso per valori maggiori o uguali a (-3+√17)/2

Logaritmi

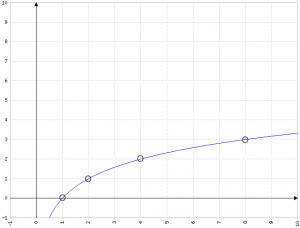
Proprietà comuni dei logaritmi

• Log_a1=0
• Log_a(xy)=Log_a(x)+Log_a(y)
• Log_a(x/y)=Log_a(x)-Log_a(y)
• Log_ax^y=y·Log_a(x)
• Log_a(1/x)=Log_a(x)^-1=-1·Log_a(x)