I cinque algoritmi sui grafi da sapere
Kruskal, Prim, Dijkstra, Bellman-Ford, Floyd-Warshall
Kruskal
L'amico Kruskal vuole trovare l'albero (o gli alberi) che collega i vertici tramite gli archi più leggeri possibile.
Per fare questo, divide i vertici di un grafo in tanti sottoinsiemi quanti sono i vertici, poi ordina gli archi e considera le coppie di vertici partendo dall'arco più leggero: se i vertici appartengono allo stesso insieme, ignora l'arco; altrimenti aggiunge l'arco all'albero di copertura e unisce i due sottoinsiemi.
Il risultato è un albero di copertura minimo, il tempo di esecuzione è Θ(E log E).
_(, )
1. ← ∅
2. ℎ ∈ [] //per [] intendiamo l’insieme dei vertici di
3. _() //abbiamo creato insiemi, ognuno dei quali contiene un vertice
4. ℎ // tipico degli algoritmi Greedy
5. ℎ (, ) ∈ [] //che sono ordinati
6. _() ≠ _() ℎ
7. ← ∪ {(, )}
8. (, )
9.
Prim
L'amico Prim vuole trovare l'albero (o gli alberi) che collega i vertici tramite gli archi più leggeri possibile.
Per fare questo, sceglie uno dei vertici e lo inserisce nell'albero, poi controlla quale tra gli archi adiacenti è il più leggero (o i più leggeri), aggiunge il vertice all'albero e gli attribuisce un peso pari all'arco. Se durante la visita un vertice è già stato visitato, ma ha un peso maggiore dell'arco corrente, si cambia l'arco connesso e si aggiorna il peso del vertice.
Il risultato è un albero di copertura minimo, il tempo di esecuzione è O(E V log V) a patto di utilizzare per l'archiviazione dell'elenco dei vertici uno heap di Fibonacci.
_(, , )
1. ← [] //inizializziamo Q con tutti i vertici di G
2. ℎ ∈
3. [] = ∞
4. [] = 0
5. [] =
6. ℎ ≠ ∅
7. ← _() //estrae il vertice con campo key minore
8. ℎ ∈ [] //per ogni vertice adiacente al vertice estratto
9. ∈ && (, ) < [] ℎ
10. [] ← //u diventa il padre di v
11. [] ← (, ) //aggiorna il valore di key e riorganizza l’heap
12. = {(, []) | ∈ \ {}}
Dijkstra
L'amico Dijkstra vuole raggiungere nel tempo/spazio minore un vertice partendo da un altro vertice.
Per fare questo, come l'amico Dijkstra, inizializza tutti i vertici con peso ∞ e parent = NIL, poi iniziando dal vertice sorgente imposta nei vertici adiacenti il peso degli archi. Se arriva a un vertice già esplorato, ma il peso del vertice è maggiore del vertice "nuovo padre" più l'arco che li congiunge, ne cambia il padre e aggiorna il peso del vertice (rilassamento).
Il risultato è un albero in cui ciascun vertice è collegato alla sorgente con il percorso più breve possibile. Il costo dipende dall'implementazione dell'elenco dei vertici, e segue questa tabella:
| Grafo sparso | Grafo denso | |
|---|---|---|
| Array lineare | O(n2) | O(n2) |
| Heap binario | O(n log n) | O(n2 log n) |
dove per "Grafo sparso" si intende un grafo in cui il numero di vertici e il numero di archi tende ad essere uguale E = Θ(V), mentre per "Grafo denso" si intende che E = Θ(V2).
NOTA: Dijkstra si incasina se ci sono archi con peso negativo.
__(, )
1. ℎ ∈ []
2. [] ← +∞
3. [] ←
4. [] ← 0
(, , )
1. [] > [] + (, ) ℎ
2. [] ← [] + (, ) //aggiorna il peso del cammino da a
3. [] ← //aggiorna il predecessore
(, , )
1. __(, )
2. ← ∅ //insieme dei vertici già estratti
3. ← [] //vertici da estrarre
4. ℎ ≠ ∅
5. ← _()
6. ← ∪ {} // S si riempie
7. ℎ ∈ []
8. (, , (, ))
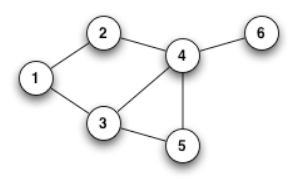
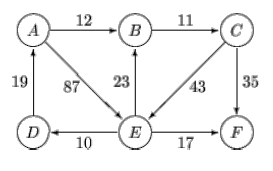
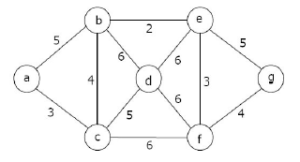
Esempio
- V(G) = {1};
- (1,2), π(2) = NIL → 1, d(2) = ∞ → 2;
- (1,3), π(3) = NIL → 1, d(3) = ∞ → 4
- V(G) = {1, 2, 3};
- i nodi esplorati sono:
- π(1) = NIL, d(1) = 0
- π(2) = 1, d(2) = 2
- π(3) = 1, d(3) = 4
- (2, 4), π(4) = NIL → 2, d(4) = ∞ → d(2) + 7 = 9
- (2, 3), π(3) = 1 → 2, d(3) = 4 → d(2) + 1 = 3
- (3, 5), π(5) = NIL → 3, d(5) = ∞ → d(3) + 3 = 6
- i nodi esplorati sono:
- V(G) = {1, 2, 3, 4, 5}
- i nodi esplorati sono:
- π(1) = NIL, d(1) = 0
- π(2) = 1, d(2) = 2
- π(3) = 2, d(3) = 3
- π(4) = 2, d(4) = 9
- π(5) = 3, d(5) = 6
- (5, 4), π(4) = 2 → 5, d(5) = 9 → d(5) + 2 = 8
- (5, 6), π(6) = NIL → 5, d(6) = ∞ → d(5) + 5 = 11
- (4, 6), π(6) = 5 → 4, d(6) = ∞ → d(4) + 1 = 10
- i nodi esplorati sono:
Bellman-Ford
Gli amici Bellman e Ford vogliono raggiungere nel tempo/spazio minore un vertice partendo da un altro vertice, ma in un grafo che può avere pesi negativi.
Uno dei motivi per cui i grafi con pesi negativi sono più incasinati di quelli con pesi solo positivi è che se c'è un ciclo e il suo bilancio è negativo (es. a→b = +2, b→a = -5) per ridurre il peso del cammino basta ciclare all'infinito il loop.
L'algoritmo è piuttosto semplice: per ogni vertice per ogni arco applica il rilassamento; poi controlla che per ogni arco il suo peso sia minore o uguale della somma del vertice più l'arco che li congiunge. In caso contrario è di fronte a un cappio con bilancio negativo e l'algoritmo si ferma restituendo falso.
Il costo dipende dal tipo di grafo, se sparso o denso:
| Grafo sparso | Grafo denso | |
|---|---|---|
| Dijkstra - Array lineare | O(n2) | O(n2) |
| Dijkstra - Heap binario | O(n log n) | O(n2 log n) |
| Bellman-Ford | O(n2) | O(n3) |
_(, , ) 1. __(, ) 2. = 1 |[]| − 1 3. ℎ (, ) ∈ [] 4. (, , (, )) 5. ℎ (, ) ∈ [] 6. [] > [] + (, ) ℎ 7. 8.
Floyd-Warshall
Gli amici Floyd e Warshall vogliono raggiungere nel tempo/spazio minore qualunque vertice partendo da un altro vertice qualunque, cioè vogliono calcolare tutti i percorsi minimi possibili.
In modo simile a una matrice M di adiacenza, creano una matrice n*n tale con w: E→R che per ogni cella i,j:
- se i == j allora M[i, j] = 0
- se i != j e (i, j) è un arco, allora M[i, j] = w(i, j)
- se i != j e (i, j) non è un arco, allora M[i, j] = ∞
Per ogni vertice controllano se la somma di ciascun vertice entrante più ciascun vertice uscente ha un peso minore dell'arco diretto o del valore calcolato precedentemente.
Il costo spaziale di questo algoritmo è n2, perché abbiamo bisogno di iniziare con quella che - di fatto - è una matrice nxn di adiacenza. Il costo temporale dell'algoritmo è n3, perché per ogni arco (compresi quelli con valore ∞, cioè compresi gli archi "assenti", che quindi corrispondono a ogni coppia nxn) dobbiamo iterare ogni vertice.
Esempio
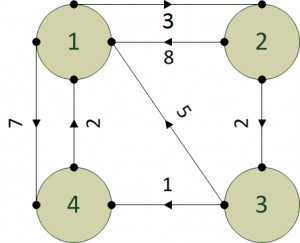
La matrice di partenza richiede che siano valorizzati tutti gli archi e che gli "auto-archi" siano impostati a zero.
| A | |||||
|---|---|---|---|---|---|
| DA | 1 | 2 | 3 | 4 | |
| 1 | 0 | ∞ | ∞ | ∞ | |
| 2 | ∞ | 0 | ∞ | ∞ | |
| 3 | ∞ | ∞ | 0 | ∞ | |
| 4 | ∞ | ∞ | ∞ | 0 | |
Gli archi da nodo verso se stesso sono impostati a zero
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 3 | ∞ | 7 |
| 2 | 8 | 0 | 2 | ∞ |
| 3 | 5 | ∞ | 0 | 1 |
| 4 | 2 | ∞ | ∞ | 0 |
Gli altri archi sono riportati (senza calcoli). Gli archi rimanenti, che non esistono, sono impostati a infinito.
Passaggio vertice 1: si riportano gli zeri, tutta la riga 1 e tutta la colonna 1, poiché rappresentano archi diretti che non è neccessario calcolare.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 3 | ∞ | 7 |
| 2 | 8 | 0 | ||
| 3 | 5 | 0 | ||
| 4 | 2 | 0 |
Ora cerchiamo di calcolare il cammino da 2 a 3. L'arco diretto riporta il peso 2, dobbiamo capire se arrivare da 2 a 3 passando per 1 è più conveniente. (2,1) pesa 8, (1, 3) pesa infinito, 8+∞ = ∞, quindi ci conviene tenere l'arco diretto.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 3 | ∞ | 7 |
| 2 | 8 | 0 | 2 | |
| 3 | 5 | 0 | ||
| 4 | 2 | 0 |
Ora cerchiamo di calcolare il cammino da 2 a 4. L'arco diretto riporta il peso ∞, dobbiamo capire se arrivare da 2 a 4 passando per 1 è più conveniente. (2,1) pesa 8, (1, 4) pesa 7, 8+7 = 15, quindi ci conviene passare per 1.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 3 | ∞ | 7 |
| 2 | 8 | 0 | 2 | 15 |
| 3 | 5 | 0 | ||
| 4 | 2 | 0 |
Da 3 a 2 l'arco diretto è ∞, mentre passando per 1 è 5+3 = 8, quindi cambiamo in 8.
Da 3 a 4 l'arco diretto è 1, mentre passando per 1 è 5+7 = 12, quindi teniamo 1.
Da 4 a 2 l'arco diretto è ∞, mentre passando per 1 è 2+3 = 5, quindi cambiamo in 5.
Da 4 a 3 l'arco diretto è ∞, mentre passando per 1 è 2+∞ = ∞, quindi lasciamo ∞.
| 1 | 2 | 3 | 4 | |
|---|---|---|---|---|
| 1 | 0 | 3 | ∞ | 7 |
| 2 | 8 | 0 | 2 | 15 |
| 3 | 5 | 8 | 0 | 1 |
| 4 | 2 | 5 | ∞ | 0 |
Partendo da questa tabella, si ripete per gli altri tre vertici.
_() 1. ← [] //calcolo il numero di righe, ovvero il numero di vertici 2. 0 = 3. = 1 4. = 1 5. = 1 6. [,]() = min([,](−1) + [,](−1), [](−1)) 7.