Le disequazioni pongono un limite, un confronto tra due quantità, e la sfida è rendere costante una delle due quantità, cioè trasformare la disequazione in qualcosa di simile a x>n, con n noto (es. x>9/5).
In una disequazione le operazioni più comuni sono la somma (sottrazione) e il prodotto (divisione) per entrambi i membri, per esempio:
3x+5>0 diventa, sommando -5 a entrambi i membri, -5+3x+5>0-5, che diventa, dividendo entrambi i membri per 3: 3x/3>-5/3 e quindi x>-5/3
Un'altra operazione comunissima è il cambio del segno (o moltiplicazione per -1). Cambiare di segno, o moltiplicare per un numero negativo, comporta che anche il verso della disequazione cambi.
Infatti, se -x>5 allora x<-5:
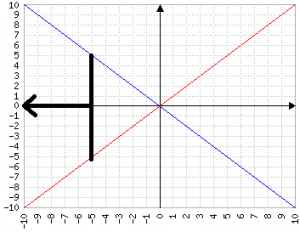
In comune con le equazioni, in cui può essere importante capire gli zeri in espressioni del tipo 3x+5=0, ci sono il campo di esistenza e i prodotti/divisioni.
Il campo di esistenza prevede le "solite" tre regole (in ℝ):
- se c'è una radice quadrata, la base deve essere ≥ 0
- se c'è un logaritmo, l'argomento deve essere > 0
- se c'è una divisione, il denominatore deve essere ≠ 0
Quindi:
√(1-x2) richiede che -1≤x≤1
1/√(1-x2) richiede anche che x≠-1 e x≠1, quindi la C.E. è -1<x<1 (minore in senso stretto)
ln(x)/√(1-x2) richiede che x sia > 0, quindi il dominio si restringe a 0<x<1
Quando in un espressione sono presenti dei prodotti il risultato deriva dallo studio del segno per esempio come x-1>0 è evidente che x-1>0 ∀ x>1.
Un'espressione come (x-1)(x+3) invece è positiva quando i segni di entrambe le espressioni sono uguali (positivi o negativi) e negativa quando sono diversi.
x-1 è positiva per x>1
x+3 è positiva per x>-3
Solitamente si fa un piccolo schema di questo genere:
-3 1 x-1>0 -----|-----0+++++ x+3>0 -----0+++++|+++++ f(x) +++++0-----0+++++
La prima espressione è positiva per valori > 1, la seconda per valori > -3, quindi hanno lo stesso segno (-) per x<-3 e (+) per x>1 e segno diverso per i valori tra -3 e 1. Per i valori -3 e 1 il valore è zero.
Ultimo appunto riguarda le disequazioni che coinvolgono valori assoluti, per cui è necessario unire le soluzioni con l'espressione con v.a. positiva con quelle con v.a. negativo.
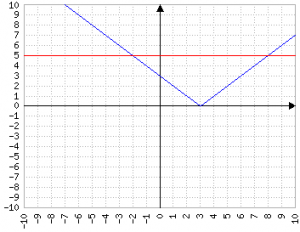
La soluzione di |x-3|>5 sono per x>0 x-3>5 e per x<0 -(x-3)>5, quindi nel primo caso x>8 e nel secondo caso -x+3>5 ⇒ x-3<5 ⇒ x<-2, coerentemente con l'immagine.