...che poi i flussi, spogliati dei formalismi, non sono mica così difficili da capire.
La dico con parole mie, parole semplici.
Il problema del massimo flusso si applica a un grafo orientato (ciascun arco ha un verso) in cui esistono due nodi "speciali", detti sorgente e pozzo, in cui rispettivamente sono presenti solo archi uscenti (sorgente) e solo entranti (pozzo).
Formalmente:
- Il grafo è denominato G(V,E). La denominazione è standard: G indica il grafo, V l'insieme dei vertici, E l'insieme degli archi.
- Gli archi si chiamano s (sorgente), t (pozzo), poi gli altri sono numerati progressivamente
- Un arco è indicato da due numeri tra parentesi separati da virgola; l'ordine determina il verso. Per esempio, (2,3) è l'arco che va dal nodo 2 al nodo 3.
- (u,v) ∈ ω-(v) indica l'insieme dei nodi che entrano in v
- (v,k) ∈ ω+(v) indica l'insieme dei nodi che escono da v
Ogni arco è caratterizzato da una capacità e da un flusso, e il flusso non può mai eccedere la capacità. Si può immaginare un tubo in cui, senza cambiare la pressione, può passare una quantità massima di acqua; da zero al massimo, il flusso può prendere qualsiasi valore (anche se negli esercizi è sempre un valore intero).
La somma di tutti i flussi entranti in un nodo è uguale alla somma dei flussi uscenti. Mantenendo la metafora, tanta acqua entra, tanta acqua esce.
Formalmente:
- 0≤xuv≤cuv (x è il flusso, c è la capacità)
- ∀v∈V-{s, t}
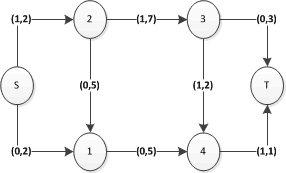
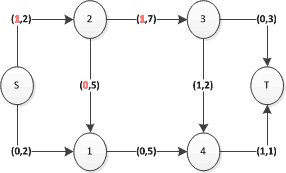
Esempio di flusso
Questo flusso è ammissibile, perché esistono un nodo s con soli archi uscenti e un nodo t con soli archi entranti, il flusso di ogni arco è compreso tra zero e la capacità; inoltre la somma di tutti i flussi entranti è uguale a quella di tutti i flussi uscenti per ciascun nodo (tranne s, t):
- entra 0, esce 0
- entra 1, esce 1
- entra 1, esce 1
- entra 1, esce 1
Il problema del massimo flusso consiste nel determinare il flusso massimo che può transitare attraverso gli archi del grafo, con le seguenti semplici regole:
- un flusso può transitare lungo il verso della freccia se il flusso è minore della capacità. In questo caso, è possibile incrementare il flusso fino ad arrivare alla capacità massima.
- un flusso può "transitare" in verso opposto rispetto alla freccia, a patto che "scali" un flusso esistente. In questo caso, si parla di "cammino aumentante"
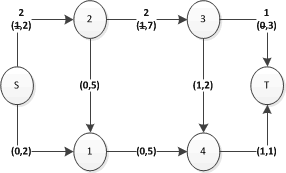
Nel caso dell'esempio, è possibile incrementare il percorso P1 = {s, (s,2), 2, (2,3), 3, (3,t), t}, poiché tutti gli archi hanno un flusso minore della capienza. Il nuovo risultato è:
Ora (s,2) è diventato impraticabile, perché il flusso è pari alla capienza.
Si può procedere con P2 = {s, (s,1), 1, (1,4), 4...
ma poi, arrivati a 4 si trova un flusso pari alla capienza, per arrivare a T. Per fortuna, è possibile "togliere 1" al flusso (3,4) e procedere poi con (3,t):
P2 = {s, (s,1), 1, (1,4), 4, (3,4), 3, (3,t), t}
Nella notazione del cammino aumentante, l'arco percorso al contrario è rappresentato secondo il suo verso, quindi anche se si va da 4 a 3, l'arco è rappresentato come (3,4).
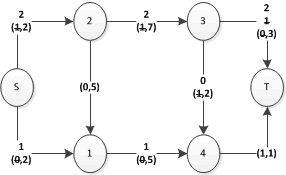
Il nuovo risultato è:
Ora il flusso uscente da s è 3, e qualunque strada porta o a un arco diretto saturo (es. (s,2)) o a un arco inverso vuoto (es. (1,2)).
Se, partendo da s, consideriamo tutti gli archi che avrebbero ancora capacità, dividendo il grafo in due otteniamo il cosiddetto taglio a capacità minima. In questo esempio, (s,2) è escluso; (s,1) è incluso; (1,2) è escluso; (1,4) è incluso; (2,3) è escluso; (3,4) è escluso; ovviamente gli archi connessi con t sono tutti esclusi (altrimenti si potrebbe aumentare il flusso). Il totale dei flussi che escono dal taglio minimo per entrare nell'insieme del pozzo è uguale al totale del flusso uscente da s.
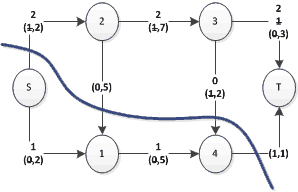
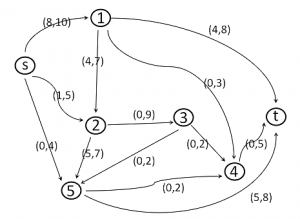
Esempio di compito (08/01/2015)
Il grafo è ammissibile, poiché tutti i nodi hanno flusso positivo e non maggiore della capacità; inoltre la somma dei flussi entranti è pari alla somma dei flussi uscenti per tutti i nodi tranne s e t.
Il grafo ha valore 9 [(s,1) = 8, (s,2) = 1, (s,5) = 0, la somma è 9].
Il grafo può essere incrementato per il percorso P1 = {s, (s,1), 1, (1,t), t} di 2.
La nuova situazione è (la prima coppia è l'arco; la seconda è flusso/capacità; sono colorati gli archi cambiati)
(s,1) = (10,10) (1,t) = (6,8) (s,2) = (1,5) (s,5) = (0,4) (1,2) = (4,7) (2,5) = (5,7) (2,3) = (0,9) (3,5) = (0,2) (5,4) = (0,2) (5,t) = (5,8) (1,4) = (0,3) (3,4) = (0,2) (4,t) = (0,5)
Può essere ancora incrementato per il percorso P2 = {s, (s,2), 2, (2,3), 3, (3,4), 4, (4,t), t} di 2.
La nuova situazione è
(s,1) = (10,10) (1,t) = (6,8) (s,2) = (3,5) (s,5) = (0,4) (1,2) = (4,7) (2,5) = (5,7) (2,3) = (2,9) (3,5) = (0,2) (5,4) = (0,2) (5,t) = (5,8) (1,4) = (0,3) (3,4) = (2,2) (4,t) = (2,5)
Può essere ancora incrementato per il percorso P3 = {s, (s,5), 5, (5, t), t} di 3.
La nuova situazione è
(s,1) = (10,10) (1,t) = (6,8) (s,2) = (3,5) (s,5) = (3,4) (1,2) = (4,7) (2,5) = (5,7) (2,3) = (2,9) (3,5) = (0,2) (5,4) = (0,2) (5,t) = (8,8) (1,4) = (0,3) (3,4) = (2,2) (4,t) = (2,5)
Può essere ancora incrementato per il percorso P4 = {s, (s,2), 2, (2,5), 5, (5,4), 4, (4,t), t} di 2.
La nuova situazione è
(s,1) = (10,10) (1,t) = (6,8) (s,2) = (5,5) (s,5) = (3,4) (1,2) = (4,7) (2,5) = (7,7) (2,3) = (2,9) (3,5) = (0,2) (5,4) = (2,2) (5,t) = (8,8) (1,4) = (0,3) (3,4) = (2,2) (4,t) = (4,5)
A questo punto, apparentemente non c'è più niente, perché (s,1) e (s,2) sono impraticabili e (5,u) ha tutti gli archi uscenti saturi. Ma usando il cammino aumentato, c'è una "via d'uscita" in (2,5)!
Può essere quindi ancora incrementato per il percorso P5 = {s, (s,5), 5, (2,5), 2, (1,2), 1, (1,t), t)} di 1.
La nuova situazione è
(s,1) = (10,10) (1,t) = (7,8) (s,2) = (5,5) (s,5) = (4,4) (1,2) = (3,7) (2,5) = (6,7) (2,3) = (2,9) (3,5) = (0,2) (5,4) = (2,2) (5,t) = (8,8) (1,4) = (0,3) (3,4) = (2,2) (4,t) = (4,5)
A questo punto tutti gli archi uscenti da s sono saturi, quindi è immediatamente evidente che si è arrivati al flusso massimo, che corrisponde a 21.
Il taglio a capacità minima è costituito solo da s.