Studio di una funzione: x/(sqrt(x)-1)

Funzione tratta da http://matepratica.tutorando.com

$\frac{x}{\sqrt{x} - 1}$

Table of Contents

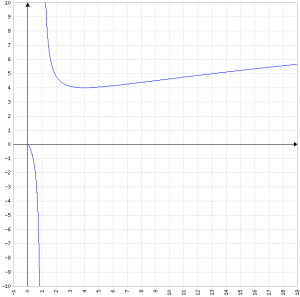
Dominio

]0, 1] ⋃ [1, +∞[

Zeri

f(x)=0 ⇒ x=0

Segno

x>0 ∀ x∈dominio
√x-1>0 ⇒ x>1
Quindi f(x)<0 nell'intervallo [0, 1] e f(x)>0 in [1, +∞[

Parità

A causa delle restrizioni sul dominio la funzione non è né pari né dispari.

Limiti

$\lim_{x \to + ∞} \frac{x}{\sqrt{x} - 1} \overset{H}{=} \frac{1}{\frac{1}{2 \sqrt{x}}} = \frac{1}{0} = + \infty$

$\lim_{x \to + ∞} \frac{x}{\sqrt{x} - 1} \cdot \frac{1}{x} = \frac{1}{\sqrt{x} - 1} = \frac{1}{\infty} = 0$

Non ci sono asintoti obliqui.

$\lim_{x \to 1^{\pm}} \frac{x}{\sqrt{x} - 1} = \frac{1}{0} = \pm \infty$

Asintoti

x=1 è un asintoto verticale.

Minimi e massimi

	Num.	Den.
Prim.	$x$	$\sqrt{x} - 1$
Der.	$1$	$\frac{1}{2 \sqrt{x}}$

[su_accordion]
[su_spoiler title="I passaggi per il numeratore" style="fancy"]

$\sqrt{x} - 1 - \frac{x}{2 \sqrt{x}}$

Moltiplico l'ultima frazione per √x/√x

$\sqrt{x} - 1 - \frac{x \sqrt{x}}{2 x}$

Semplifico x/x

$\sqrt{x} - 1 - \frac{\sqrt{x}}{2}$

Sommo le radici:

$\frac{\sqrt{x}}{2} - 1$

Metto a fattor comune:

$\frac{\sqrt{x} - 2}{2}$

Sposto il /2 al denominatore, e ottengo il risultato finale:

[/su_spoiler]
[/su_accordion]

$\frac{\sqrt{x} - 2}{2 {(\sqrt{x} - 1)}^{2}}$

Il denominatore è composto da una costante e da un'espressione al quadrato, che quindi può essere solo ≥ 0.

Il numeratore determina il segno, che è negativo per valori compresi tra ±4 (ma il dominio ha come minimo zero!).

Il punto (4, 4) è un punto di minimo locale.

	Num.	Den.
Prim.	$\sqrt{x} - 2$	$2 {(\sqrt{x} - 1)}^{2}$
Der.	$\frac{1}{2 \sqrt{x}}$	[su_accordion] [su_spoiler title="I passaggi per il calcolo della derivata" style="fancy"] Per il momento lasciamo perdere il 2 che moltiplica tutto, lo aggiungeremo alla fine. Una delle possibilità è moltiplicare √x-1 per se stesso. Si ottiene $x - 2 \sqrt{x} + 1$ . Essendo una somma posso derivare i singoli pezzi. $(x)' = 1$ $(- 2 \sqrt{x})' = - \frac{2}{2 \sqrt{x}} = - \frac{1}{\sqrt{x}}$ $(1)' = 0$ Reintroduco il 2 che avevo messo da parte all'inizio. Wolfram suggerisce anche di derivare per sostituzione. Secondo me è più complicato, ma vediamo lo stesso. $u = \sqrt{x} - 1$ $(2 u^{2})' = 4 u$ Per tornare da u a x è necessario sostituire √x-1 a u e moltiplicare per la derivata dell'espressione che sostituisco. $(\sqrt{x} - 1)' = \frac{1}{2 \sqrt{x}}$ Sostituisco √x-1 a u e moltiplico per la derivata di √x-1. $\frac{4 (\sqrt{x} - 1)}{2 \sqrt{x}}$ Semplifico dividendo numeratore e den. per 2: $\frac{2 (\sqrt{x} - 1)}{\sqrt{x}}$ moltiplico il 2 al numeratore: $\frac{2 \sqrt{x} - 2}{\sqrt{x}} = \frac{2 \sqrt{x}}{\sqrt{x}} - \frac{2}{\sqrt{x}}$ Semplificando √x/√x ottengo il risultato. [/su_spoiler] [/su_accordion] $2 - \frac{2}{\sqrt{x}}$

Num.

Den.

Prim.

\sqrt{x} - 2

2 {(\sqrt{x} - 1)}^{2}

Der.

\frac{1}{2 \sqrt{x}}

[su_accordion]
[su_spoiler title="I passaggi per il calcolo della derivata" style="fancy"]
Per il momento lasciamo perdere il 2 che moltiplica tutto, lo aggiungeremo alla fine.
Una delle possibilità è moltiplicare √x-1 per se stesso. Si ottiene

x - 2 \sqrt{x} + 1

.
Essendo una somma posso derivare i singoli pezzi.

$(x)' = 1$

$(- 2 \sqrt{x})' = - \frac{2}{2 \sqrt{x}} = - \frac{1}{\sqrt{x}}$

$(1)' = 0$

Reintroduco il 2 che avevo messo da parte all'inizio.

Wolfram suggerisce anche di derivare per sostituzione. Secondo me è più complicato, ma vediamo lo stesso.

$u = \sqrt{x} - 1$

$(2 u^{2})' = 4 u$ Per tornare da u a x è necessario sostituire √x-1 a u e moltiplicare per la derivata dell'espressione che sostituisco.

$(\sqrt{x} - 1)' = \frac{1}{2 \sqrt{x}}$ Sostituisco √x-1 a u e moltiplico per la derivata di √x-1.

$\frac{4 (\sqrt{x} - 1)}{2 \sqrt{x}}$ Semplifico dividendo numeratore e den. per 2:

$\frac{2 (\sqrt{x} - 1)}{\sqrt{x}}$ moltiplico il 2 al numeratore:

$\frac{2 \sqrt{x} - 2}{\sqrt{x}} = \frac{2 \sqrt{x}}{\sqrt{x}} - \frac{2}{\sqrt{x}}$ Semplificando √x/√x ottengo il risultato.

[/su_spoiler]
[/su_accordion]

$2 - \frac{2}{\sqrt{x}}$

Troppe radici! I calcoli diventano tutti più leggibili se si sostituisce una variabile alla radice di x. Poniamo t=√x.

	Num.	Den.
Prim.	$t - 2$	$2 {(t - 1)}^{2}$ oppure $2 t^{2} - 4 t + 2$
Der.	$1$	$4 t - 4$

Num.

Den.

Prim.

t - 2

2 {(t - 1)}^{2}

oppure

$2 t^{2} - 4 t + 2$

Der.

1

4 t - 4

Il risultato intermedio è

$\frac{2 t^{2} - 4 t + 2 - (t - 2) (4 t - 4)}{{(2 {(t - 1)}^{2})}^{2}}$

Il denominatore è [su_tooltip content="Il denominatore è sempre > 0 tranne quanto t=1. Quando t=1, x=1²=1, che però è esterno al dominio. Quindi in realtà il denominatore è sempre > 0 in senso stretto"] sempre ≥0 [/su_tooltip], quindi mi concentro sul numeratore:

$2 t^{2} - 4 t + 2 - 4 t^{2} + 4 t + 8 t - 8 = - 2 t^{2} + 8 t - 6 = - 2 (t^{2} - 4 t + 3)$

-2 è costante e non influisce sul calcolo degli zeri.

$\frac{4 \pm \sqrt{16 - 12}}{2} = \frac{4 \pm 2}{2} = 2 \pm 1$

Gli zeri (di t) sono in corrispondenza di 3 e 1, e tra 1 e 3 t>0.

Essendo t=√x, f"(x)>0 tra 1² e 3², cioè tra 1 e 9.

Quindi da 0 a 1 (escluso perché non in dominio) la funzione è concava, da 1 (escluso) a 9 è convessa, a x=9 c'è un flesso, poi diventa sempre concava.

Nota: in realtà nell'asintoto in x=1 è presente un cambio di concavità, perché per x<1 tende a -∞ e per x>1 tende a +∞, ma comunque questo cambio di concavità non è un vero e proprio flesso.

Grafico della funzione

$1fracsqrtx-1$