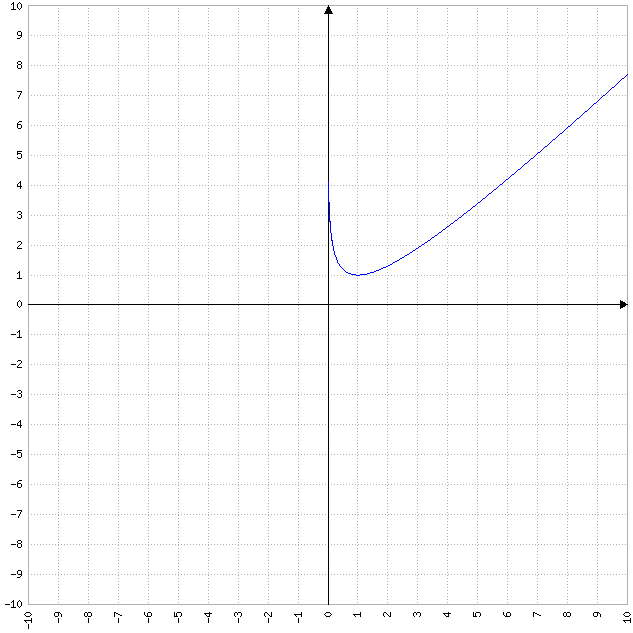
Funzione tratta da http://matepratica.tutorando.com
Table of Contents
Commento
La funzione è composta da due parti distinte: x e ln(x), che hanno i seguenti grafici "base":
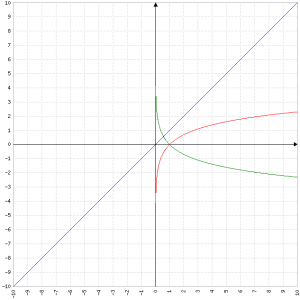
in rosso y=ln(x) (non fa parte della funzione)
in verde y=-ln(x)
Dominio
Il dominio è ℝ+, che corrisponde ai numeri reali strettamente positivi (cioè senza lo zero), poiché ln(x) ha come dominio ℝ+.
Zeri
f(x)=0 ⇒ x=ln(x)
Come si vede dal grafico, x è sempre maggiore di ln(x) nel dominio, quindi la funzione non interseca mai l'asse delle ascisse.
Siccome x=0 è esterno al dominio, la funzione non interseca nemmeno l'asse delle ordinate, quindi non ci sono zeri.
Simmetrie
Siccome la funzione ha dominio ℝ+ non può essere pari né dispari.
Segno
La funzione è sempre positiva. Una possibile prova è risolvere la funzione per un caso particolare (es. f(1) = 1) e constatare che non ci sono zeri né asintoti (tranne l'asintoto a zero, valido solo a destra), quindi non cambia mai di segno.
Limiti
Il limite per x che tende a zero è + ∞, perché -ln(x), che tende a infinito, cresce molto più velocemente di x, che tende a zero.
Abbiamo due "parti" che tendono entrambe a infinito, ma di segno opposto.
Graficamente vediamo che y=x tende all'infinito più velocemente di -ln(x), ma come lo dimostriamo?
De l'Hôpital funziona solo con le frazioni, e qui non ne abbiamo, ma...
x tende all'infinito, 1 tende a... 1, mentre a ln(x)/x possiamo (finalmente) applicare De l'Hôpital, ottenendo
che tende a zero velocemente.
Perciò, per tornare al quesito iniziale, ora siamo sicuri che
Verifichiamo l'eventuale presenza di un asintoto obliquo:
infatti x/x=1 e il limite di ln(x)/x è zero, come visto sopra.
Ora verifichiamo il termine costante dell'eventuale asintoto obliquo:
f(x) - mx
x-ln(x)-x = -ln(x), il cui limite per +∞ è +∞
Quindi non c'è asintoto obliquo.
Asintoti
x=0 è un asintoto verticale.
Minimi/massimi
Il minimo locale si calcola tramite la derivata: quando vale zero significa che siamo di fronte a un minimo.
f'(x) = 1-1/x, che è minore di zero per x > 1, è maggiore di zero per x < 1 ed è zero per x=1
Quindi la funzione decresce da 0 a 1, tocca un minimo in x=1, f(x)=1 e poi cresce.
Punti di flesso
f"(x) = 0+1/x2, che è > 0 per ogni x ∈ dominio.
La funzione è sempre convessa e non ha punti di flesso.
Grafico della funzione