Studio di una funzione: (e^(1-x))/(x^2-1)

Funzione tratta da http://matepratica.tutorando.com

$\frac{e^{1-x}}{x^2-1}$

Forme alternative

$\frac{e^{1-x}}{\left(x+1\right)·\left(x-1\right)}$

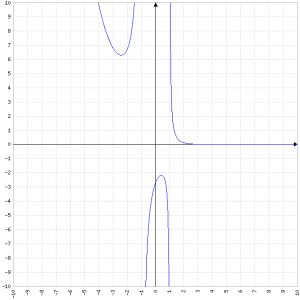
Dominio

ℝ \ {±1}

Zeri

f(x) = 0 ⇒ e^1-x = 0, ma e^n è sempre positivo, quindi y≠0 ∀ x∈ℝ

Se x = 0, f(x) = -e

Segno

Il numeratore è sempre > 0.
Il denominatore è una parabola con vertice rivolto in basso, quindi è negativa solo per l'intervallo ]-1, 1[
f(x) > 0 per x compreso tra -1 e 1, non ha senso per x = ±1 e infine > 0 per x < -1 ⋃ x > 1

Parità

$\frac{e^{1-\left(-x\right)}}{{\left(-x\right)}^2-1}=\frac{e^{1+x}}{x^2-1}$

quindi f(x) non è né pari né dispari.

Limiti

Il limite per ±∞ è (applicando de l'Hôpital)

$\underset{x\to \pm \infty }{\lim }\frac{e^{1-x}}{x^2-1}=\frac{0}{\infty }\stackrel{\text{H}}{=}\underset{x\to \pm \infty }{\lim }\frac{-e^{1-x}}{2x}\stackrel{\text{H}}{=}\underset{x\to \pm \infty }{\lim }\frac{e^{1-x}}{2}=0$

Il limite per ±1 è

$\underset{x\to -1^{\mp }}{\lim }\frac{e^{1-x}}{x^2-1}=\pm \infty$

e viceversa:

$\underset{x\to +1^{\mp }}{\lim }\frac{e^{1-x}}{x^2-1}=\mp \infty$

Asintoti

Sono presenti un asintoto orizzontale in corrispondenza di x = 0 e due asintoti verticali in corrispondenza di ± 1.

Minimi e massimi

	f(x)	g(x)
P	$e^{1-x}$	$x^2-1$
D	$-e^{1-x}$	$2x$

Si può direttamente raggruppare per

$-e^{1-x}$

in questo modo:

$\frac{-e^{1-x}\left(x^2+2x-1\right)}{{\left(x^2-1\right)}^2}$

Ora:

$-e^{1-x}$

è sempre negativo per qualunque esponente,

${\left(x^2-1\right)}^2$

è sempre positivo

$x^2+2x-1$

è positivo per i valori esterni a

$\frac{-2\pm \sqrt{4+4}}{2}=-1\pm \sqrt{2}$

La funzione quindi decresce fino a -1-√2, poi cresce fino a -1+√2, poi torna a decrescere.
Presenta un punto di minimo a -1-√2 e un punto di massimo a -1+√2

Grafico della funzione