Studio di una funzione: (3-x^2)/(x-2)^2

Funzione tratta da http://matepratica.tutorando.com

$\frac{3-x^2}{{\left(x-2\right)}^2}$

Altre forme

$\frac{3-x^2}{x^2-4x+4}$

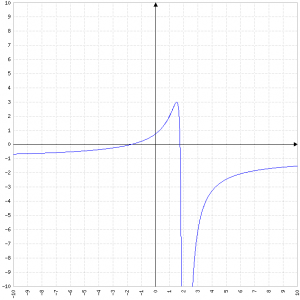
Dominio

ℝ\{2}

Zeri

f(x) = 0 ⇒ 3-x^2 = 0 ⇒ x^2 = 3 ⇒ x = ±√3
Inoltre f(0) = 3/4

Parità

Dal momento che esiste un asintoto verticale in +2, non è possibile che la funzione sia pari né dispari.

Segno

Il numeratore è > 0 solo nell'intervallo (-√3, +√3)
Il denominatore è > 0 in ℝ tranne in 2, che è fuori dal dominio.
f(x) < 0 per valori di x inferiori a -√3 e superiori a +√3, escluso 2
f(x) > 0 per valori di x compresi tra -√3 e +√3.

Asintoti

x=2 è un asintoto verticale
y=-1 è un asintoto orizzontale

Limiti

$\underset{x\to \pm \infty }{\lim }\frac{3-x^2}{{\left(x-2\right)}^2}=\frac{\sout{x^2}\left(\boxed{\frac{3}{x^2}}-1\right)}{\sout{x^2}\left(1-\boxed{\frac{4}{x}}+\boxed{\frac{4}{x^2}}\right)}$

Gli elementi nei riquadri rossi tendono a zero e si possono ignorare.

Quindi i limiti per ±∞ sono entrambi -1.

$\underset{x\to 2}{\lim }\frac{3-x^2}{{\left(x-2\right)}^2}=\frac{-1}{0}=-\infty$

Sia a sinistra sia a destra di 2 il numeratore è negativo e il denominatore è positivo, quindi il limite è da entrambi i lati negativo.

Minimi e massimi

	Num.	Den.
Prim.	$3-x^2$	${\left(x-2\right)}^2$
Der.	$-2x$	$2\left(x-2\right)$

Posso raccogliere x-2 al numeratore e abbassare il denominatore di un grado (da 4 a 3):

$\frac{\sout{\left(x-2\right)}\left(-2x\left(x-2\right)-6+2x^2\right)}{{\left(x-2\right)}^{\sout{4}3}}$

sviluppo il numeratore:

$\frac{\sout{-2x^2}+4x-6+\sout{2x^2}}{{\left(x-2\right)}^3}$

il numeratore > 0 per x > 3/2
il denominatore > 0 per x > 2
f'(x) è > 0 da -∞ a 3/2 e da 2 a +∞ ed è negativa solo tra 3/2 e 2, quindi 3/2 è massimo locale (il punto è (3/2, 3)) e la funzione è sempre crescente tranne tra 3/2 e 2 (2 non è minimo né massimo perché non è in dominio).

Flessi

Cerchiamo almeno un flesso: se il limite per -∞ è -1, esiste un massimo a y=3 e poi la funzione tende a -∞ per x=2 significa che c'è almeno un cambio di direzione.

	Num.	Den.
Prim.	$4x-6$	${\left(x-2\right)}^3$
Der.	$4$	$3{\left(x-2\right)}^2$

Raccolgo (x-2)^2 e semplifico con il denominatore

$\frac{\sout{{\left(x-2\right)}^2}\left(4x-8-12x+18\right)}{{\left(x-2\right)}^{\sout{6}4}}$

Siccome il denominatore è sempre positivo, tranne per x=2, che è zero, devo verificare il segno del numeratore.

-8x+10 = 2(-4x+5) ⇒ il 2 è costante, quindi posso non considerarlo

-4x+5>0 ⇒ -4x>-5, cambio il segno e inverto il verso:

4x<5 rarr="" x="" 5="" 4="" p="">

Esiste un punto di flesso in x=5/4; con x<5/4 il grafico è convesso, con x>5/4 il grafico è concavo.

Grafico della funzione