Studio di una funzione: (2x-1)/(x-3)

Funzione tratta da http://matepratica.tutorando.com

$\frac{2x-1}{x-3}$

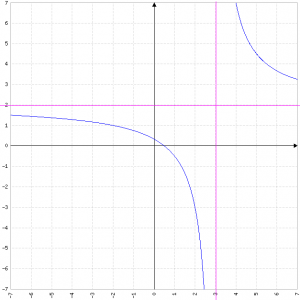
Dominio

Il dominio è ℝ tranne i valori di x per cui il denominatore è zero.

In questo caso x-3=0 ⇒ x=3.
Il dominio è quindi ℝ\{3}

Zeri

La funzione vale zero quando il numeratore vale zero e x è nel dominio.
In questo caso 2x-1=0 ⇒ x=1/2
L'unico punto per cui la funzione passa per l'ascissa è quindi P₁=(1/2, 0)

Se x=0 la funzione vale -1/-3 = 1/3
L'unico punto per cui la funzione passa per l'ordinata è quindi P₂=(0, 1/3)

Simmetrie

$\frac{2\left(-x\right)-1}{\left(-x\right)-3}=\frac{-2x-1}{-x-3}\ne \text{f(x) e}\ne \text{-f(x)}$

La funzione non è né pari né dispari.

Asintoti

L'asintoto è presente quando c'è un punto di discontinuità di primo o secondo tipo.
In questo caso il punto di discontinuità è nel punto x=3, e siccome il numeratore con x=3 è diverso da zero, siamo in presenza di un asintoto verticale.

Segno

Il segno è positivo quando c'è concordanza di segni tra il numeratore e il denominatore.

                        1/2     3
Num: 2x-1>0 ⇒ x>1/2  -      +      +
-------------------------+------+------
Den: x-3>0 ⇒ x>3     -      -      +
-------------------------+------o------
f(x)                 +   |   -  φ   +

Considerazioni

In base agli elementi riscontrati finora, la funzione ha un valore positivo per x<1/2, passa per il punto (1/2, 0), poi diventa negativa e tende a -∞ a sinistra di x=3, che è asintoto verticale. A destra, l'asintoto tende a +∞, poi la funzione resta positiva sempre.

Limiti

Si dimostra che

$\underset{x\to \mathrm{3^\pm}}{\lim }f\left(x\right)=\pm \infty$

Preso un numero m∈ℝ, m>0, f(x) con x che tende a 3 da destra sarà sempre maggiore di M.

$|\frac{2x-1}{x-3}\mathrm{}|>M$

Considero il caso 1 (limite sinistro a +∞):

$\frac{2x-1}{x-3}\mathrm{}>M$

Porto M a sinistra:

$\frac{2x-1}{x-3}-M>0$

Moltiplico M per (x-3)/(x-3) e metto a fattor comune:

$\frac{2x-1-Mx+3M}{x-3}>0$

Raccolgo x:

$\frac{x\left(2-M\right)-1+3M}{x-3}>0$

Posso togliere il denominatore, perché ho già escluso dal dominio x=3:

$x\left(2-M\right)-1+3M>0$

Passo a destra tutto quanto non è x:

$x>\frac{1+3M}{2-M}$

Raccolgo M a destra:

$x>\frac{\sout{M}\left(\frac{1}{M}-3\right)}{\sout{M}\left(\frac{2}{M}-1\right)}$

Dal momento che 1/M e 2/M tendono a zero posso escluderle dal mio calcolo (in particolare, con M > 0, l'espressione è > 3, con M crescente, 1/M decresce, l'espressione si avvicina da destra a 3).

Con M sempre più grande, il limite si avvicina a -3/-1, che è uguale a 3, CVD.

---

Considero il caso 2 (limite destro a -∞):

$\frac{2x-1}{x-3}\mathrm{}<-M$

Porto M a sinistra:

$\frac{2x-1}{x-3}+M<0$

Moltiplico M per (x-3)/(x-3) e metto a fattor comune:

$\frac{2x-1+Mx-3M}{x-3}<0$

Raccolgo x:

$\frac{x\left(2+M\right)-1-3M}{x-3}<0$

Posso togliere il denominatore, perché ho già escluso dal dominio x=3:

$x\left(2+M\right)-1-3M<0$

Passo a destra tutto quanto non è x:

$x<\frac{1+3M}{2+M}$

Raccolgo M a destra:

$x<\frac{\sout{M}\left(\frac{1}{M}+3\right)}{\sout{M}\left(\frac{2}{M}+1\right)}$

Dal momento che 1/M e 2/M tendono a zero posso escluderle dal mio calcolo (in particolare, con M > 0, l'espressione è > 3, con M crescente, 1/M decresce, l'espressione si avvicina da sinistra a 3).

Con M sempre più grande, il limite si avvicina a 3, CVD.

---

Limite orizzontale

Per x→±∞ il limite è dimostrato brevemente:

$\underset{x\to \pm \infty }{\lim }\frac{2x-1}{x-3}=+2$

poiché

$\underset{x\to \pm \infty }{\lim }\frac{\sout{x}\left(2\boxed{-\frac{1}{x}}\right)}{\sout{x}\left(1\boxed{-\frac{3}{x}}\right)}=2$

x si semplifica e i riquadri in rosso tendono a zero e quindi si possono ignorare.

Minimi e massimi

La derivata di una funzione razionale è data dalla formula:

$\left(\frac{f\left(x\right)}{g\left(x\right)}\right)\text{'}=\frac{f\text{'}\left(x\right)g\left(x\right)-f\left(x\right)g\text{'}\left(x\right)}{{\left(g\left(x\right)\right)}^2}$

Nel nostro caso:

	f(x)	g(x)
funz.	2x-1	x-3
der.	2	1

Dato che interessa lo studio del segno, conviene non sviluppare il denominatore (g(x)²)

La derivata è quindi:

$\frac{2\left(x-3\right)-\left(2x-1\right)}{{\left(x-3\right)}^2}$

cioè

$-\frac{5}{{\left(x-3\right)}^2}$

che è sempre negativa (il numeratore è una costante negativa, il denominatore un valore per definizione positivo).

Quindi la funzione scende sempre e non ha punti stazionari.

Punti di flesso

La derivata seconda della funzione è

	f(x)	g(x)
funz.	-5	(x-3)^2
der.	0	2(x-3)

$\frac{10x-30}{{\left(x-3\right)}^4}$

Il denominatore è sempre positivo e non influenza il segno.

Al numeratore, raccolgo 10 e ottengo x-3: x-3 > 0 quando x > 3, quindi la funzione è concava per valori < 3 e convessa per valori > 3.

Grafico