Studio di una funzione: 1/(2x^2+3x-5)

Funzione tratta da http://matepratica.tutorando.com

$\frac{1}{2x^2+3x-5}$

Zeri dell’espressione di II grado

Applichiamo la formula per gli zeri dell'espressione di II grado:

$\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Nel nostro caso, a=2, b=3, c=-5

$\frac{-3\pm \sqrt{3^2-4·2·-5}}{2·2}$

quindi:

$\frac{-3\pm 7}{4}$

Il Δ è positivo, quindi le soluzioni sono due: -5/2 e 1.

Noti gli zeri, il denominatore si può quindi scrivere anche come:
(2x+5)(x-1)

Dominio

Il dominio è ℝ tranne i valori di x per cui il denominatore è zero.

Dominio = ℝ\{-5/2, 1}

Zeri

L'unico zero è nel punto P=(0, -1/5).

Simmetrie

La funzione non è né pari né dispari.

Si può notare infatti che il numeratore è costante e il denominatore ha sia un elemento di grado II diverso da zero sia un elemento di grado I, la funzione non può essere pari; inoltre essendo di secondo grado non può nemmeno essere dispari.

Segno

Dato che il numeratore è costante, il segno dipende unicamente dal denominatore.

x² ha segno positivo, quindi l'espressione è > 0 per gli intervalli esterni agli zeri:

f(x) > 0 per ]-∞, -1/5[ ∨ ]1, +∞[

Limiti

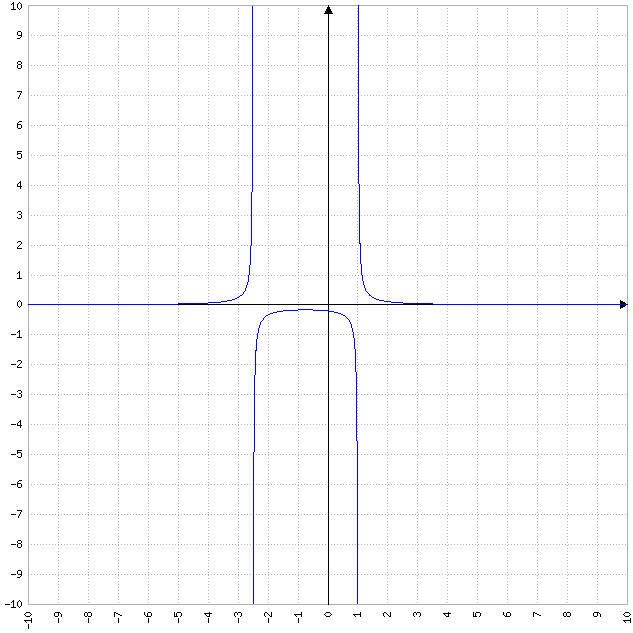
Dallo studio degli zeri si capisce che i limiti verticali sono diversi a destra e a sinistra in entrambi i casi.

$\underset{x\to {-\frac{1}{5}}^{\pm }}{\lim }\frac{1}{2x^2+3x-5}=\mp \infty$

uguale a

$\underset{x\to {-\frac{1}{5}}^{\pm }}{\lim }\frac{1}{0}=\mp \infty$

al contrario,

$\underset{x\to 1^{\pm }}{\lim }\frac{1}{2x^2+3x-5}=\pm \infty$

---

Il limite per ±∞ è

$\underset{x\to \pm \infty }{\lim }\frac{1}{2x^2+3x-5}=\underset{x\to \pm \infty }{\lim }\frac{1}{x\left(2\boxed{+\frac{3}{x}}\boxed{-\frac{5}{x^2}}\right)}$

Le due espressioni cerchiate tendono a zero e si possono ignorare; anche 2, che è costante, si può ignorare, perché per x sempre più grande il limite tende sempre più a zero⁺.

Asintoti

Sono presenti due asintoti verticali in corrispondenza dei punti esterni al dominio e un asintoto orizzontale corrispondente all'asse delle ascisse.

Minimi e massimi

Si applica la formula della derivata di 1/f(x):

$\left(\frac{1}{f\left(x\right)}\right)\text{'}=-\frac{f\text{'}\left(x\right)}{{\left(f\left(x\right)\right)}^2}$

quindi

$\frac{4x+3}{{\left(2x^2+3x-5\right)}^2}$

Lo studio del segno è semplice, perché il denominatore è sempre < 0 nel dominio della funzione.

Quindi la derivata ha segno negativo per x>-3/4 e la funzione ha un massimo locale in P_min=(-3/4, -49/8).

Punti di flesso

La derivata seconda della funzione è

	f(x)	g(x)
funz.	4x+3	(2x^2+3x-5)2 oppure (2x+5)2(x-1)2
der.	4	2(2x2+3x-5)(4x+3)

Grafico