Il problema che la distribuzione ipergeometrica si propone di risolvere riguarda la probabilità che uno o più successi (in statistica, il "successo" non porta necessariamente una connotazione positiva) accadano in un numero di eventi in seguito a un numero di rilevazioni.
Per esempio in una popolazione di 30 studenti, di cui 17 maschi e 13 femmine siano chiamate a essere interrogate tre persone di cui esattamente due maschi.
La popolazione è indicata con N, e corrisponde, nell'esempio, a 30.
I successi sono indicati con K, e corrispondono, nell'esempio, a 2 (ovviamente si poteva scegliere di considerare "successo" anche 1, ribaltando la domanda: quante probabilità di interrogare esattamente una femmina su tre interrogati).
Il numero di rilevazioni è indicato con n ed è 3.
Notiamo che chiamando 15 persone (tutte le femmine + due maschi) non è possibile arrivare a non interrogare esattamente due maschi in nessun caso: possiamo ottenere, seppure con probabilità scarsa, fino a 13 femmine e 0 maschi oppure 14 femmine e 1 maschio, ma all'estrazione successiva restano solo maschi.
P(n = (1-K)+k) = 1.
Notiamo anche che chiamando una sola persona non possiamo ottenere sicuramente due maschi.
P(n < k) = 0
Infine il numero di estrazioni deve essere minore o uguale al numero di elementi.
n ≤ N
Alla prima chiamata, possiamo ottenere un maschio oppure una femmina
Maschio P(1) = 17/30
Femmina 1-P(1) = (30-17)/30
La seconda chiamata dipende dall'esito della prima, e questo distingue la distribuzione ipergeometrica da molte altre distribuzioni: la distribuzione ipergeometrica "ha memoria".
La seconda estrazione si fa su un campione non più di 30, ma di 29 elementi, in quanto uno (maschio o femmina che sia) è stato estratto.
Per quanto riguarda i successi, il numero di possiblità cambia in base all'estrazione precedente: 17 successi se l'estrazione precedente è stata scelta una femmina; 16 viceversa.
La probabilità di estrarre un maschio è quindi "biforcata":
Se la prima estrazione è uscito un maschio, è di 16/29, se la prima è uscita una femmina è di 17/29; quindi la probabilità di avere due maschi è di 17/30*16/29 (˜31,2%).
Sommando la probabilità che alla seconda sia uscita una femmina 13/30*13/29 (˜25,4%) e la probabilità che alla prima estrazione sia uscita una femmina 13/30 (˜43,3%), si ottiene 1: infatti è sicuro che su due estrazioni sia uscita una femmina al primo turno oppure un maschio e uno tra maschio o femmina al secondo.
Le estrazioni possono essere rappresentate come un albero binario, in cui a ogni estrazione si sceglie di seguire il percorso di sinistra in caso di successo o destra in caso di insuccesso (anche questa è una convenzione, senza considerazioni di merito).
A ogni passo dell'albero, le informazioni che cambiano sono il numero di elementi del campione (decrementa a ogni livello dell'albero), il numero di successi (si decrementa solo nel ramo di sinistra), il cumulo di percentuale di probabilità, che moltiplica le probabilità precedenti fino alla radice.
Per il nostro problema, che è di trovare la probabilità che escano due elementi maschi su tre, ci viene in aiuto il coefficiente binomiale, che ci dice che le combinazioni utili sono 1, 3, 3, 1, ovvero 1 sequenza che porta a tre maschi, 3 che portano a due maschi e una femmina, 3 a due femmine e un maschio e 1 che porta a tre femmine (1: {MMM}; 3: {MMF, MFM, FMM}; 3: {FFM, FMF, MFF}; 1: {FFF}).
Le probabilità che ci interessa contare sono quelle del secondo gruppo: MMF, MFM, FMM.
MMF:
Alla prima estrazione abbiamo 30 elementi, 17 successi, una probabilità accumulata nulla, quindi la probabilità di successo è 17/30.
Alla seconda abbiamo 29 elementi, 16 successi, una probabilità accumulata di 17/30, quindi una probabilità di successo di 16/29 * 17/30 = 272/870.
Alla terza abbiamo 28 elementi, 15 successi, una probabilità accumulata di 272/870 e dobbiamo calcolare la probabilità che esca una femmina, che è di 13/28; la probabilità di successo è quindi di 3.536/24.360.
MFM:
Prima: abbiamo 30 el, 17 succ, p.a. nulla, p(M) = 17/30.
Seconda: abbiamo 29 el, 16 succ, p.a. 17/30, ci interessa la probabilità che esca femmina, che è 13/29, il totale è 17/30*13/29 = 221/870.
Terza: abbiamo 28 el, 16 succ. p.a. 221/870, ci interessa la probabilità che esca maschio, che è 16/28, il totale è 221/870*16/28= 3.536/24.360
FMM:
Prima: abbiamo 30 el, 17 succ, p.a. nulla, p(F) = 13/30
Seconda: abbiamo 29 el, 17 succ, p.a. 13/30, P(M) = 17/29, p. tot = 221/870.
Terza: abbiamo 28 el, 16 succ. p.a. 221/870, ci interessa la probabilità che esca maschio, che è 16/28, il totale è 221/870*16/28= 3.536/24.360
Sommando tre volte 3.536 si ottiene 10.608, che diviso per 24.360 dà 0,43546...
Notiamo che la probabilità che si ottenga MMF, MFM o FMM è identica, perché anche se le percentuali di probabilità cambiano, alla fine abbiamo sempre 17, 16, 13 al numeratore e 30, 29, 28 al denominatore.
I dati che ci interessano per generalizzare la formula sono:
- 30 * 29 * 28, che è N! / (N-n)!
- 17 * 16 * 13, che è il prodotto di K! / (K-k)! e (N-K)! / (N-K-n+k)!
- 3, che è il coefficiente binomiale di (2 3), cioè i casi di successo desiderati sulle estrazioni
Il risultato è dato dal prodotto di questi termini:
rappresenta il numero di esiti positivi che vogliamo ottenere (nell'esempio, 17*16)
rappresenta il numero di esiti negativi utili a completare il numero di estrazioni (nell'esempio, 13, ma se fossero state più estrazioni sarebbero 13*12*11...)
è rappresentabile anche come
è il numero di risultati corrispondenti al nostro requisito (2 maschi su 3 persone).
Da notare che il numero di femmine (1 femmina su 3 persone), cioè
dà lo stesso risultato; in generale, portando il concetto in formula:
è l'inverso - poiché sta al denominatore - del numero totale di esiti possibili (nel nostro esempio 1/(30*29*28)).
Moltiplicando tutto, si ottiene
La formula è già incasinata così come sta, ma è necessario porre un'ulteriore limitazione:
che rappresenta il fatto che, se estraiamo 14 persone, sicuramente estraiamo almeno un maschio, N-K-n+k potrebbe essere un valore negativo.
Table of Contents
Formula semplificata
Dopo aver "sbattuto" contro questa formula, la formula "semplificata" sembrerà quasi abbordabile, pur essendo costituita da ben tre coefficienti binomiali:
Basta riscrivere la formula a coefficienti binomiali come formula con i fattoriali, secondo l'equivalenza
per ottenere praticamente la funzione da cui siamo partiti.
Excel
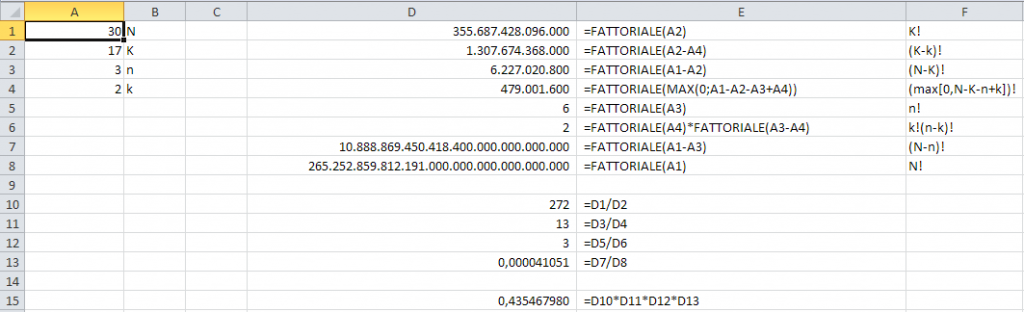
Di seguito, uno screenshot di un foglio excel in cui è riportato tutto il ragionamento sotto forma di formule
Calcolare velocemente distribuzioni ipergeometriche semplici
Quando un problema è posto come
c'è una popolazione di N elementi, di cui K sono successi: quante probabilità ho di ottenere k successi su n estrazioni?
sono di fronte a un problema risolvibile con la distibuzione ipergeometrica. Purtroppo il calcolo di un coefficiente binomiale come quello dell'esempio richiede di calcolare 30! e 27!, che sono numeri enormi.
È possibile calcolare il risultato di un problema abbastanza semplice ragionando in questo modo:
- Al numeratore metto una serie discendente di numeri che rappresentano le probabilità di successo (nell'esempio 2 probabilità di successo = 17*16) e le moltiplico per la serie discendente di insuccessi, fino ad avere un prodotto di n numeri, dove n è il numero di estrazioni (nell'esempio, 17*16*13)
- Al denominatore metto una serie discendente di popolazione, da 1 a n (nell'esempio, 30*29*28).
- Ottengo due serie di prodotti con lo stesso numero di termini (nell'esempio, 3 termini al numeratore e 3 al denominatore: 17*16*15 / 30*29*28).
- Moltiplico per il coefficiente binomiale, ma - se i numeri sono piccoli - posso arrivarci anche ragionando: ho 8 possibilità diverse (MMM, MMF, MFM, MFF, FMM, FMF, FFM, FFF), di cui 3 di ottenere esattamente 2 maschi e una femmina.