Mi sono trovato quasi per caso alla lezione odierna di MD, e mi è piaciuta molto.
L'argomento che ha tenuto banco per tutta la sera è l'insieme ℤ, con un'attenzione particolare alla corrispondenza con gli elementi dell'insieme ℕ. Pur senza dirlo esplicitamente, si è dimostrato che la cardinalità dei due insiemi è sempre ℵ0.
Il discorso, iniziato evidentemente la lezione precedente, è partito da come rappresentare l'insieme ℤ conoscendo solo l'insieme ℕ. In pratica, i numeri ℤ sono rappresentabili in un piano cartesiano di naturali ℕXℕ in cui i numeri sono rappresentati in uno dei tre modi:
- [n+1,1] ⇒ +n
- [1,1] ⇒ 0
- [1,n+1] ⇒ -n
In pratica ogni numero positivo è rappresentato dalla coppia [n+1, 1], ogni numero negativo da [1, n+1] e lo zero da [1,1].
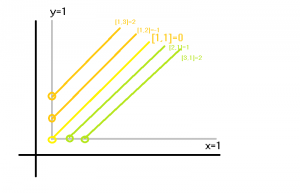
In realtà ogni "retta diagonale" rappresenta un numero, positivo o negativo, e ogni numero nella forma [n+1,m+1] è riconducibile a una delle tre forme sottraendo [1,1].
Sottrarre [1,1] (che equivale a zero) non cambia il significato del numero rappresentato. Per esempio, [4,2] rappresenta lo stesso numero di [3,1] = +2, a cui si può arrivare sottraendo [1,1] una o più volte.
Un altro esempio è [4,7], a cui sottraendo [1,1] più volte si può ricondurre prima [3,6], poi [2,5] e infine [1,4] = -3.
La dimostrazione che [a,b]+[1,1] = [a,b] è la seguente.
Poiché due numeri [a,b] e [c,d] con a,b,c,d ∈ ℕ sono equivalenti se a+d = b+c (graficamente, si trovano sulla stessa "retta diagonale", cioè nella stessa classe di equivalenza), [a+1,b+1] = [a,b] se a+1+b = b+1+a, che è evidentemente vero.
Poiché rappresentare i numeri come n oppure come [n+1,1] è equivalente, le proprietà dei numeri interi restano identiche indipendentemente dalla notazione, anche se le dimostrazioni sono diverse.
Per esempio, è già dimostrato sopra che zero è elemento neutro per la somma.
È anche l'elemento che trasforma in zero qualunque numero tramite moltiplicazione; in notazione matematica:
∀ n∈ℤ n x 0 = 0
Dobbiamo dimostrare quindi che [n,m] x [1,1] = [1,1]
Sviluppando, [n,m] x [1,1] = [nx1 + mx1, nx1, mx1] ≃ [1,1].
Inoltre ∀ z∈ℤ, &Exist; un unico z1∈ℤ tale che z+z1=0, o in altri termini una coppia [c,d] tale che [a,b]+[c,d] = [1,1]
Tale [c,d] è detto opposto ed è in realtà [b,a].
Table of Contents
Assiomi dei numeri naturali
Il prof ha parlato anche degli 11 assiomi sui numeri naturali. Cercando in giro mi sono imbattuto negli assiomi di Peano sui ℕ, ma non sono 11, ma solo 5, e includerebbero 0 (zero) nell'insieme ℕ, mentre mi pare che la scuola di pensiero corrente faccia iniziare ℕ da 1.
Il primo assioma di Peano è che esiste uno zero nei naturali: 0∈ℕ
Il secondo è che esiste una funzione "successore" S:ℕ→ℕ
Il terzo è che se x≠y allora S(x)≠S(y).
Il quarto dice che 0 non è nell'immagine di S. In pratica, non esiste "un numero il cui successore è zero" tra i ℕ. Questo, con il precedente, comporta che la funzione S è iniettiva, e quindi non è ciclica, e anche che ogni numero ha una corrispondenza biiettiva con il suo successore. In altre parole, dire 5 oppure "il numero il cui successore è 6" è la stessa cosa.
Il quinto è in pratica il principio di induzione, che dice: l'insieme ℕ è il più piccolo insieme che contenga 0 e il successore di ogni suo elemento.
Fatto questo excursus sugli assiomi di Peano (personaggio singolare di fine '800 - inizio '900, reduce dal classico, esperto di calcolo infinitesimale ma innamorato della semplicità!), gli assiomi a cui fa riferimento il prof sono altri, tanto è vero che si riferisce all'ottavo assioma per perfezionarlo perché possa funzionare anche in ℤ.
Se nxt=mxy ⇒ n=m, a patto che t sia diverso da zero.
Se questo assioma funzionava per ℕ anche senza questa precisazione è perché il prof evidentemente considera 0∉ℕ.
Altre differenze tra ℕ e ℤ
In ℕ per definire un rapporto tra due numeri n,m si dice n<m se ∃ un t∈ℕ tale che n+t=m.
Nell'insieme ℤ, dati due numeri [a,b] e [c,d] si dice che [a,b]<[c,d] se a+d<b+c (utilizzando la definizione di minore data per i naturali).
Inoltre, in ℤ non possiamo usare il principio di induzione, perché non esiste un minimo; possiamo usare un A⊂ℤ se A è dotato di minimo.
Sia X⊂ℤ, si dice che b è minorante di X se ∀ x∈X, b≤x.
Nota1: non è detto che b appartenga a X!
Nota2: non è detto che b corrisponda a un unico numero, anzi è più probabile che corrisponda all'insieme di numeri minori di un certo valore.
Se un sottoinsieme X ≠ ∅, X⊂ℤ ha un minorante, allora ha un minimo unico.
Esempio:
sia X={x∈ℤ | x mod 3 = 0}
altrimenti X={x∈ℤ, y∈ℤ | y=x·3}
non ha minorante, poiché se b∈ℤ fosse minorante di X, esisterebbe un b-1, b-2 oppure b-3 che sicuramente sarebbe divisibile per tre, e quindi sarebbe a sua volta minorante di X.
Altro esempio:
sia X={z∈ℤ | z2≤z·100}
0≤z≤100, quindi 0 è minorante dell'insieme.
Terzo esempio:
sia b minorante di X⊆ℤ, X≠∅
sia X={x∈ℤ | x+(b-1)∈X}
x+(b-1) ≥ b, da cui deriva che x-1≥0 cioè x≥1.
Perciò l'insieme X = ℕ
Altre proprietà
ℤ è dotato di uno zero, che è unico.
ogni z∈ℤ ha uno e un solo opposto; l'opposto del proprio opposto è il numero stesso.
Dati due interi a,b∈ℤ con b≠0, ∃ p,q∈ℤ tali che a=b·q+r.
Dove q è il quoziente e r è il resto.
Matematicamente r può essere un qualunque intero, ma è corretto che 0≤r<|b|
In altre parole, posso scrivere entrambe
27 = 6·4+3
27 = 6·3+9
ma la seconda è scorretta (non sbagliata): poiché 9>6 si può incrementare il quoziente per fare in modo che il resto sia compreso tra zero e il quoziente-1.