Funzioni efficienti (grafi) - 12/09/2016

Posted by On Filed under Algoritmi e strutture dati

Si stabilisca quale problema risolve il seguente algoritmo, che accetta in ingresso un grafo non orientato G = (V, E):

MyAlgorithm(G)
1. A = ∅
2. ordina i vertici di G per grado crescente
3. for each u ∈ V[G] do /* vertici estratti secondo l’ordine stabilito nel passo 2 */
4.    if MyFunction(G,A,u) then
5.       A = A ∪ {u}
6. return A
MyFunction(G,A,u)
1. for each v ∈ A do
2.    if (u,v) ∈ E[G] then
3.       return FALSE
4. return TRUE

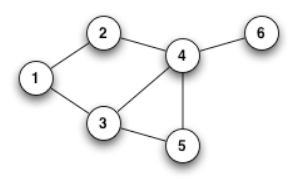
Si dimostri la correttezza dell’algoritmo, si determini la sua complessità e si simuli infine la sua esecuzione sul seguente grafo:

Svolgimento

  1. l'algoritmo restituisce l'insieme con i gradi più bassi possibile di elementi non collegati tra loro
  2. l'algoritmo è corretto, perché, essendo composto da due cicli for innestati, termina sicuramente
  3. la complessità è data da
    1. ordinamento O(n log(n))
    2. un ciclo Θ(n), che richiama un altro ciclo Θ(n), quindi il costo complessivo è Θ(n2)
    3. la ricerca dell'arco, che a seconda dell'implementazione può essere O(n) o O(log(n))
    4. la complessità totale è quindi O(n log(n)) + Θ(n2) + O(n) ⇒ O(n2)
  4. L'esecuzione:
    1. Si considera l'elemento 6: A è vuoto, quindi MyFunction restituisce true e l'elemento viene aggiunto ad A
    2. Si considera l'elemento 1: A contiene solo 6, che non è collegato a 1. L'elemento è quindi aggiunto.
    3. Si considera l'elemento 5: non è collegato ad alcun vertice in A, quindi l'elemento è aggiunto.
    4. Si considera l'elemento 2: è collegato a 1, che è presente in A, quindi l'elemento non è aggiunto.
    5. Si considera l'elemento 4: è collegato a 5 e 6, che sono presente in A, quindi l'elemento non è aggiunto.
    6. Si considera l'elemento 3: è collegato a 1 e a 5, che sono presente in A, quindi l'elemento non è aggiunto.
    7. Il risultato finale è che A contiene 1, 5, 6.