"Dritte" sugli integrali

L'integrale è l'operazione opposta alla derivata.

In pratica, se f'(x) è la derivata di f(x), allora f(x) è l'integrale di f'(x).

In realtà, quando derivo una funzione "perdo" un'informazione: per esempio la derivata di x²+4x-5 è 2x+4, l'informazione "-5" viene persa. In effetti la derivata contiene "meno informazione" rispetto all'integrale. La prova di questo è che se re-integro la funzione derivata ottengo una funzione che passa per (0, 0) e non quella originale:

$\int 2x+4\mathrm{dx}$

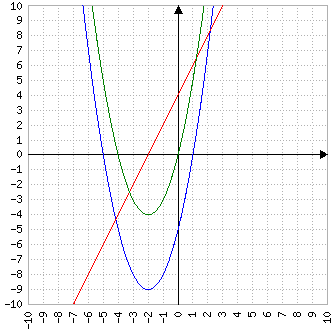
Per questo al termine del calcolo dell'integrale si aggiunge un valore costante ma ignoto che per prassi si usa chiamare C.

$\int 2x+4\mathrm{dx}=x^2+4x+C$

Nel nostro esempio, C = -5, ma la derivata è uguale anche per x²+4x-6, x²+4x-7, x²+4x+1000...

dx

dx rappresenta la derivata di x. Fino a quando non si affrontano gli integrali risolti per sostituzione, si può pensare che siccome la derivata di x è 1 moltiplicare per dx è ininfluente ai fini del risultato.

C

Quando risolviamo una derivata in realtà stiamo ottenendo non un unico risultato, ma un insieme di risultati, tutti validi, che differiscono tra loro di un valore costante.

Se conoscessimo C, data una funzione da integrare potremmo risalire esattamente alla funzione integrata.

Derivata - integrale e ritorno

Partendo dalla regola per trovare la derivata, è possibile dedurre molte regole per ottenere l'integrale corrispondente, tenendo sempre conto che derivare significa poter "perdere" dei valori costanti.

Potenze

La derivata di una potenza xⁿ è nx^n-1, quindi per esempio la derivata di x³ è 3x².
La regola vale anche per numeri negativi (si ricorda che x^-1 = 1/x, la cui derivata è -1/√2)
La regola vale anche per numeri razionali (si ricorda che x^3/2 = √x³, la cui derivata è 3/2 x^1/2 ⇒ 3√(x)/2)
La regola vale anche per numeri irrazionali (la derivata di x^π è πx^π-1)

L'integrazione di una potenza si ottiene alzando di un grado l'esponente e dividendo per l'esponente+1.

Per esempio:

$\int x^2\mathrm{dx}=\frac{x^3}{3}+C$

La correttezza si prova facendo la derivata di x³/3, che è 3x²/3 e quindi x², a cui dobbiamo aggiungere C.

Esempio un po' più difficile:

$\int \frac{1}{\sqrt[3]{x^4}}\mathrm{dx}$

In realtà l'esempio non è così difficile come sembra. Bisogna scrivere tutto sotto forma di esponente, quindi se 1/x = x^-1 e √x = x^1/2 possiamo scrivere, in modo equivalente:

$\int x^{-\frac{4}{3}}\mathrm{dx}$

Applicando la regola definita sopra, il reciproco dell'(esponente+1) moltiplica:

$\int x^{-\frac{4}{3}}\mathrm{dx}=-3\frac{1}{-\frac{4}{3}+1}\text{(...)}=\frac{1}{-\frac{1}{3}}\text{(...)}=-3\text{(...)}$

Poi si riporta x, elevata all'esponente + 1:

$\int x^{-\frac{4}{3}}\mathrm{dx}=-3x^{-\frac{4}{3}+1}=-3x^{-\frac{1}{3}}$

A questo punto, x^-1/3 lo scriviamo come reciproco (perché l'esponente è negativo) della radice terza di 3:

$\int x^{-\frac{4}{3}}\mathrm{dx}=-3\frac{1}{\sqrt[3]{x}}=-\frac{3}{\sqrt[3]{x}}$

L'ultimo passaggio è aggiungere la costante al risultato:

$-\frac{3}{\sqrt[3]{x}}+C$

Funzione con esponente derivata

Derivare una funzione con esponente significa:

1. abbassare di un grado l'esponente della funzione
2. moltiplicare per l'esponente
3. moltiplicare per la derivata della funzione

Per esempio, la derivata di (senx)⁴ ha come derivata 4(senx)³ cosx

Di conseguenza, avendo una funzione elevata a una potenza che moltiplica la sua derivata è integrabile riportando la funzione elevata alla n+1 e dividendo per l'esponente+1.

Tutto sta a riconoscere la derivata...

Esempio facile:

$\int {\left(x^2+1\right)}^{9}2x\mathrm{dx}$

Aumento di grado x²+1 e divido per l'esponente +1:

$\int {\left(x^2+1\right)}^{9}2x\mathrm{dx}=\frac{x^{10}}{10}+C$

Esempio medio:

$\int {\left(x^2+cos\left(x\right)\right)}^9\left(2x-\mathrm{sen}\left(x\right)\right)\mathrm{dx}$

Per risolvere, bisogna identificare in x^2 cos(x) la funzione (con segno positivo), e in 2x - senx la derivata della funzione. Il segno meno "migra" verso il senx, quindi l'integrale si risolve così:

$\int {\left(x^2+cos\left(x\right)\right)}^9\left(2x-\mathrm{sen}\left(x\right)\right)\mathrm{dx}=\frac{{\left(x^2+cos\left(x\right)\right)}^{10}}{10}+C$

Esempio difficile / 1: "crearsi" la derivata

$\int {\left(x^2+{\mathrm{<em>e</em>}}^x\right)}^3·\left(x+\frac{{\mathrm{<em>e</em>}}^x}{2}\right)$

In questo caso la "derivata" non è completa, perché la derivata di x^2+e^x è 2x+e^x.

Possiamo moltiplicare tutto per 1 = 2/2 = 2*1/2:

$\int {\left(x^2+{\mathrm{<em>e</em>}}^x\right)}^3·\left(x+\frac{{\mathrm{<em>e</em>}}^x}{2}\right)·2·\frac{1}{2}$

Tutto quanto è costante può essere "portato fuori" dall'integrale a nostra discrezione. Portando fuori 1/2, teniamo dentro l'integrale proprio il 2 che ci mancava:

$\frac{1}{2}\int {\left(x^2+{\mathrm{<em>e</em>}}^x\right)}^3·\left(x+\frac{{\mathrm{<em>e</em>}}^x}{2}\right)·2$

e "trasformiamo" la derivata incompleta nell'esatta derivata della funzione con la potenza:

$\frac{1}{2}\int {\left(x^2+{\mathrm{<em>e</em>}}^x\right)}^3·\left(2x+{\mathrm{<em>e</em>}}^x\right)$

questo vale

$\frac{1}{2}·\frac{1}{4}{\left(x^2+{\mathrm{<em>e</em>}}^x\right)}^4+C=\frac{1}{8}{\left(x^2+{\mathrm{<em>e</em>}}^x\right)}^4+C$

Integrazione per party

L'integrazione per parti ha origine da una considerazione sulla derivata di un prodotto (per comodità le derivate sono evidenziate in rosso scuro):
(f(x)·g(x))' = f'(x)·g(x)+f(x)·g'(x)
Essendo il prodotto e la somma commutativi, l'ordine in cui si scrive la somma o in cui si scrivono i termini dei prodotti è indifferente. (Personalmente preferisco quest'ordine perché "assomiglia" alla derivata di una divisione)

Scritta sotto forma di integrali:

$f\left(x\right)·g\left(x\right)=\int f\text{'}\left(x\right)·g\left(x\right)+f\left(x\right)·g\text{'}\left(x\right)\mathrm{dx}$

Per la nota proprietà degli integrali, un integrale di una somma è equivalente all'integrale di ciascuno dei termini, quindi si può riscrivere quanto sopra in questo modo:

$f\left(x\right)·g\left(x\right)=\int f\text{'}\left(x\right)·g\left(x\right)+\int f\left(x\right)·g\text{'}\left(x\right)$

Spostando a sinistra uno dei due integrali ottengo esattamente la formula degli integrali per parti:

$f\left(x\right)·g\left(x\right)-\int f\left(x\right)·g\text{'}\left(x\right)\mathrm{dx}=\int f\text{'}\left(x\right)·g\left(x\right)\mathrm{dx}$

L'integrazione per parti è comoda quando la "f(x)" è facilmente integrabile e ci si vuole sbarazzare di una g(x) difficile da integrare (ma facile da derivare).

Esempio:

$\int log\left(x\right)·cos\left(x\right)\mathrm{dx}$

Delle due, log(x) è più difficile da integrare di cos(x), ma è semplice da derivare (log(x))' = 1/x

$\int log\left(x\right)·cos\left(x\right)\mathrm{dx}=log\left(x\right)·sen\left(x\right)-\int \frac{1}{x}·cos\left(x\right)\mathrm{dx}$

(todo: trovare un esempio più semplice)

Un altro uso che rende l'integrazione per parti comoda è moltiplicare l'integrando... per uno! Uno è semplice da integrare e permette di trasformare una funzione difficile da integrare nella sua derivata per x.

$\int f-incasinata\left(x\right)=\int f-incasinata\left(x\right)·1\mathrm{dx}$

Integrando per parti, ottengo:

$\int f-incasinata\left(x\right)·1\mathrm{dx}=x·f-incasinata\left(x\right)-\int \left(f-incasinata\left(x\right)\right)\text{'}·x\mathrm{dx}$

Per esempio, devo integrare l'arcotangente di x (la sua derivata è 1/(1+x^2)):

$\int arctg\left(x\right)\mathrm{dx}=x·arctg\left(x\right)-\int \frac{1}{1+x^2}·x\mathrm{dx}$

Alla funzione integranda:

$\frac{x}{1+x^2}$

manca davvero poco per essere nella forma

$\frac{\mathrm{f\text{'}}\left(x\right)}{f\left(x\right)}$

Anche in questo caso posso moltiplicare per 1 = 2/2 = 2 * 1/2

$\int arctg\left(x\right)\mathrm{dx}=x·arctg\left(x\right)-\int \frac{x}{1+x^2}·2·\frac{1}{2}\mathrm{dx}$

Delle due costanti, posso portare fuori dall'integrale 1/2 e mantenere dentro il 2, così ottengo esattamente un integrale nella forma

$\frac{\mathrm{f\text{'}}\left(x\right)}{f\left(x\right)}$

cioè:

$\int arctg\left(x\right)\mathrm{dx}=xarctg\left(x\right)-\frac{1}{2}\int \frac{2x}{1+x^2}\mathrm{dx}$

Per la celebre regola

$\int \frac{\mathrm{f\text{'}}\left(x\right)}{f\left(x\right)}=ln\left|f\left(x\right)\right|+C$

il risultato finale dell'integrale è:

$\int arctg\left(x\right)\mathrm{dx}=xarctg\left(x\right)-\frac{1}{2}ln\left(1+x^2\right)+C$

Gli integrali per parti si prestano sempre a due interpretazioni. Quando è chiaro che la funzione è il prodotto di due funzioni, bisogna decidere quale delle due è quella da integrare e quale quella da considerare derivata.

$\int sen\left(x\right)x^2\mathrm{dx}$

possiamo vederla così:

funz.	der.
sen(x)	cos(x)
x^3/3	x^2

ma questo ci porterebbe ad alzare di grado la funzione e questa di solito non è una buona idea:

$sen\left(x\right)·\frac{x^3}{3}-\int cos\left(x\right)\frac{x^3}{3}\mathrm{dx}$

Proviamo a invertire le funzioni:

funz.	der.
-cos(x) (occhio al segno meno)	sen(x)
x^2	2x

$x^2\left(-cos\left(x\right)\right)-\int -cos\left(x\right)2x$

annullo il segno meno esterno all'integrale e quello interno:

$x^2\left(-cos\left(x\right)\right)+\int cos\left(x\right)2x$

Insistendo per questa strada:

funz.	der.
sen(x)	cos(x)
2x	2

$-x^{2}cos\left(x\right)+2xsen\left(x\right)-\int 2sen\left(x\right)$

Il 2 posso "portarlo fuori" e resta l'integrale di sen(x), che è -cos(x) (il segno meno si "annulla" con quello fuori dall'integrale):

$-x^{2}cos\left(x\right)+2xsen\left(x\right)+2cos\left(x\right)+C$

Integrali per sostituzione