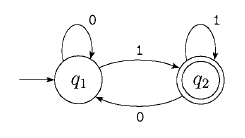
Differenze tra DFA e NFA
Le DFA e le NFA sono equivalenti, cioè ciascuna delle due può esprimere esattamente gli automi espressi dall'altra, ma ci sono alcune differenze:
- DFA deve illustrare tutte le possibili combinazioni di stati. In altre parole, per ogni stato Qn, si devono esplorare tutti gli elementi dell'alfabeto, mentre in una NFA uno stato può non essere espresso esplicitamente.
- NFA può avere, nello stesso stato, più volte lo stesso valore di alfabeto. In questo caso è necessario creare più thread, ciascuno dei quali è valido. Mentre in una DFA l'elemento accettato Qn ∈ F ⊆ Q è uno, in una NFA può essere più di uno (da chiarire! Se fosse così, gli automi non sarebbero equivalenti!)
- NFA ha un valore supplementare nell'alfabeto: ε, che rappresenta una stringa vuota. Se uno stato ha una freccia ε uscente, si creano due thread, uno sullo stato corrente e uno sullo stato di destinazione di ε.
Tra le due definizioni - simili - ci sono alcune piccole differenze.
Questa è la definizione formale di NFA
| Symbol | Meaning | Example |
|---|---|---|
| Q | finite set called the States | Come per DFA |
| Σ | finite state called Alphabet | Come per DFA |
| δ:QxΣε→P(Q) | transition function | P(Q) è il powerset di Q, cioè l'insieme di tutte le combinazioni di Q.
Σε rappresenta l'alfabeto arricchito di epsilon. |
| q0∈Q | start state | Come per DFA |
| F⊆Q | Set of accepted states | Come per DFA |