Leggevo su qualche libro che per risolvere tutte le soluzioni delle equazioni di III grado è necessario conoscere (bene) i numeri complessi ℂ, ma dopo l'ultima lezione sulle derivate improvvisamente sono diventato "esperto" di queste equazioni.
In particolare, sono rimasto molto colpito da come è possibile far corrispondere una funzione di III grado con una di II che ne rappresenta la funzione derivata.
Per esempio, se voglio sapere la derivata di
il cui grafico è
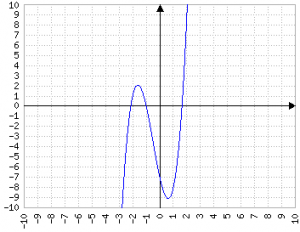
applicando la regola per le derivate: axn ⇒ naxx-1
2x3 ⇒ 6x2
3x2 ⇒ 3x
6x ⇒ 6 (sarebbe 6·1·x0)
L'equazione di II grado della derivata è quindi:
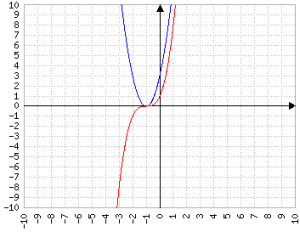
il cui grafico è
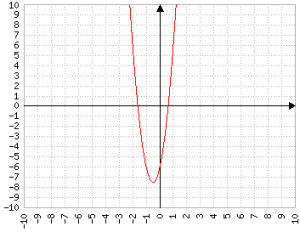
Sovrapponendo le due equazioni sembrano non avere niente in comune...
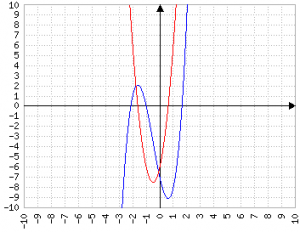
...eppure impostando due "guide" scopriamo che le "soluzioni" dell'equazione di secondo grado corrispondono ai punti in cui la derivata dell'equazione di III grado vale zero:
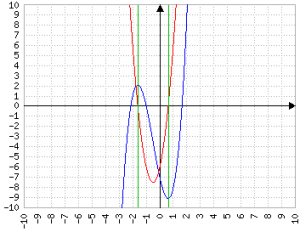
Due conti veloci e scopriamo che gli zeri dell'equazione di II grado sono
ma a dire il vero il risultato importa poco.
L'importante è la riflessione successiva: se le soluzioni dell'equazione di II grado descrivono i punti in cui la derivata dell'equazione di III grado corrispondente, cosa succede se il Δ è zero? E se è negativo?
Facile: con Δ=0 la funzione ha un solo punto di derivata zero, se Δ<0 la funzione ha derivata sempre positiva o sempre negativa.
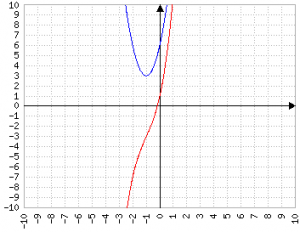
È una scoperta straordinaria per me. Il delta delle equazioni di II grado - che ormai un po' conosco - ha un significato indiretto nelle equazioni di terzo.
Questo significa che il Δ delle "facili" e2 rappresenta l'esistenza di un solo zero - se Δ è ≤ 0 - o di due o tre zeri.
Soluzioni
Considerata l'equazione ax^3+bx^2+cx+d, il segno di a indica il verso del grafico: se a è positivo, il grafico cresce (localmente può anche scendere, ma presa una scala sufficientemente grande, diciamo 1/100 del valore di a si vede l'andamento generico in maniera piuttosto chiara), se è negativo scende.
Inoltre più piccolo è a e più b "conta", quindi l'"ansa" della parabola è marcata. In particolare, se b è positivo, l'ansa è rivolta a sinistra, se b è negativo è rivolta a destra:
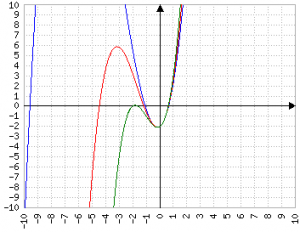
blu=a piccolo
rosso=a medio
verde=a grande
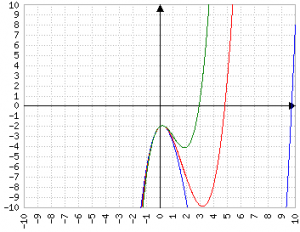
blu=a piccolo
rosso=a medio
verde=a grande
Aumentare b comporta che la "gobba" (sicuramente ci saranno definizioni migliori) si accentui: questo è ovvio, perché il primo membro (a), come già detto sopra, "vince alla lunga" sempre, ma in un'area sufficientemente piccola b si mette in evidenza.
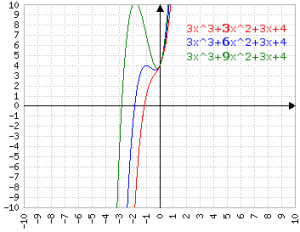
Alla fin fine, nella funzione derivata b rappresenta il termine elevato al quadrato nel delta, e se ne "percepisce" l'importanza:
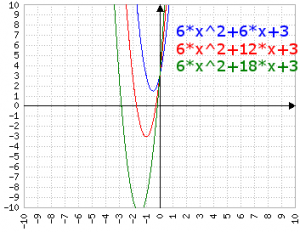
Il valore di c cambia l'altezza della gobba in maniera inversamente proporzionale (aumenta c, diminuisce la gobba), al punto che con un c sufficientemente elevato l'equazione può passare da tre a una soluzione, alla stessa maniera con cui il c nell'equazione di secondo grado, se aumenta, può "alzare" la parabola talmente tanto da non farla più intersecare con l'ascissa.
In ogni caso, il cambiamento del valore di c non modifica - come nell'equazione di II grado - il punto y per x=0:
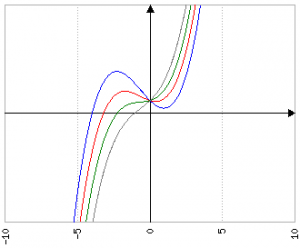
Ovviamente il significato dell'ultimo termine, quello costante, qualunque sia il grado della funzione, contribuisce solo ad "alzare" o "abbassare" tutto, senza aggiungere niente di interessante.
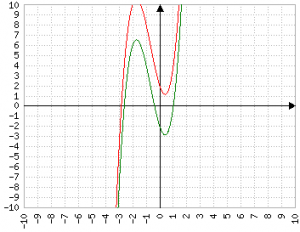
(ci penso un po' su e poi integro con altro)