I prof tendono a essere precisi e a dare definizioni esatte, soprattutto quelli di matematica.
Però questi appunti si possono chiamare, in confidenza, anche "funzioni con la x sotto" o "funzioni con l'incognita al divisore".
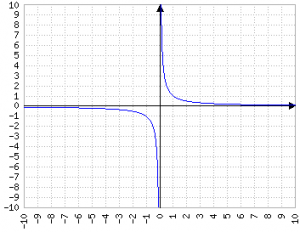
e rappresenta il grafico della proporzionalità inversa: più aumenta x e più cala y, anche se né x né y arrivano mai a zero, perché l'altro asse arriverebbe all'infinito.
1/x è molto semplice ed elegante, perché è simmetrico lungo la retta y=-x e in tutte le direzioni tende agli assi dell'ascissa e dell'ordinata (cioè y=0 e x=0).
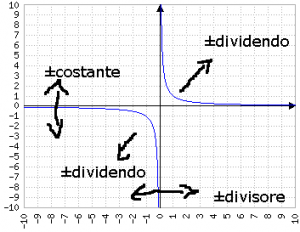
Aggiungere un numero costante:
non fa altro che "alzare" così come sta le iperboli nel primo e terzo quadrante, facendo sì che tendano a y=1, y=2... y=n invece che y=0:
Anche aggiungere x al dividendo fa "alzare" l'iperbole (1+1/x = (x+1)/x)
Togliere un valore costante, ovviamente, fa abbassare l'iperbole.
Se invece cambiamo di segno la frazione, facendo diventare negativo 1/x, la parabola si specchia lungo l'asse delle ordinate:
Per "spostare" a destra o sinistra l'iperbole basta aggiungere o togliere unità dal divisore:
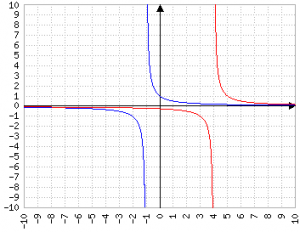
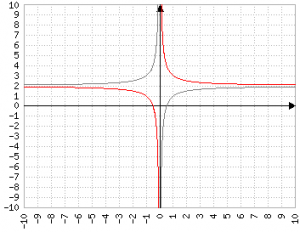
Attenzione! Scrivere 1/(x+1) oppure 1/(1+x) è lo stesso, perché la somma è commutativa; al contrario 1/(x-4) o 1/(4-x) da due risultati molto diversi, anzi specchiati:
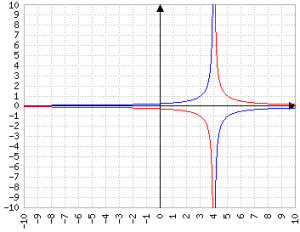
y=1/(x-4) (rosso)
y=1/(4-x) (blu)
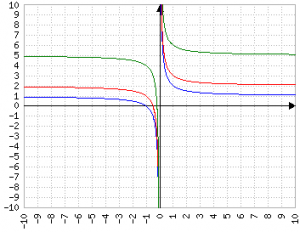
Infine, aumentare il dividendo fa "allargare" l'iperbole:
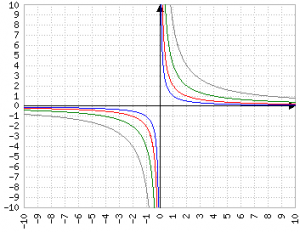
y=1/x (blu)
y=2/x (rosso)
y=4/x (verde)
y=8/x (grigio)
Più diminuisce il dividendo e più l'iperbole "si appiattisce" sull'asse delle ascisse, perché si avvicina a una retta costante in cui qualunque valore di x porta a 0.
Inoltre più si assomigliano dividendo e divisore e più l'iperbole assomiglia a una retta in cui la variabile "conta" meno.
Per es. 3x/x è una retta costante = 3, con dominio ℝ\{0}
Mettere al dividendo una funzione di secondo grado crea due coppie di "iperboli deformate", con punti di accumulazione nelle due soluzioni della parabola:
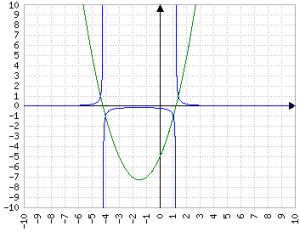
Ovviamente, con Δ=0 c'è solo un punto di accumulazione e con Δ<0 gli unici limiti sono ±∞