Le equazioni nella forma
producono una certa varietà di curve.
Si possono classificare principalmente in base al valore dei delta (Δ) del numeratore e del denominatore.
Il Δ di un'equazione di secondo grado rappresenta i punti in cui interseca l'asse delle ascisse.
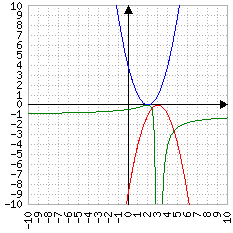
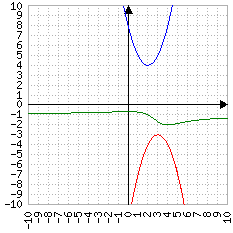
Anche graficamente, si può vedere che - a seconda dell'equazione - può intersecare l'asse delle ascisse una, due o nessuna volta:
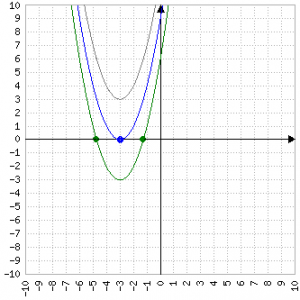
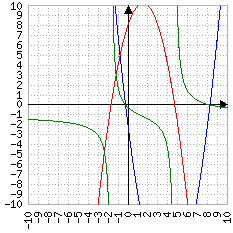
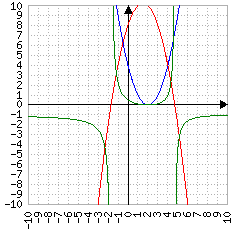
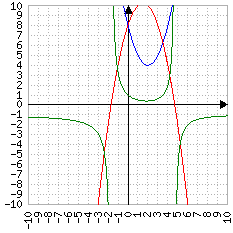
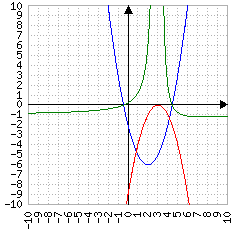
Blu: un punto
Verde: due punti
Quando una parabola (il grafico dell'equazione di secondo grado) interseca l'asse delle ascisse f(x) vale zero. Δ rappresenta la "distanza" tra le due soluzioni, cioè tra i due punti in cui vale zero: se la distanza è zero significa che il punto è uno solo (in blu, nell'immagine), se vale più di zero significa che ci sono due punti distanti tra loro Δ; se vale meno di zero significa che non ci sono punti di cui calcolare la distanza, perché la parabola è sempre positiva (o negativa)
Abbiamo quindi tre possibilità al numeratore e tre al denominatore, per un totale di nove possibilità:
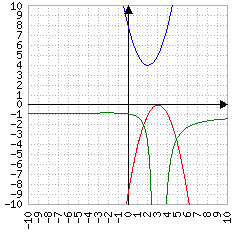
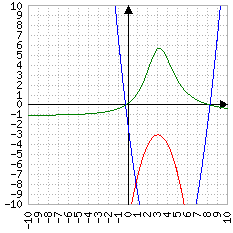
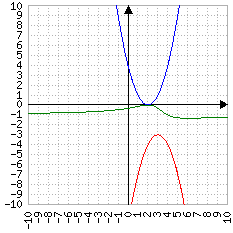
| Numeratore (in blu) | ||||
|---|---|---|---|---|
| Δ>0 | Δ=0 | Δ<0 | ||
|
Denominatore (in rosso) |
Δ>0 |
|
|
|
| Δ=0 |
|
|
|
|
| Δ<0 |
|
|
|
|
Osservazioni
Dal numeratore possiamo desumere dove la funzione vale zero, cioè dove passa attraverso l'asse delle ascisse.
Dal denominatore possiamo desumere se e dove ci sono degli asintoti verticali, perché se il denominatore vale zero la funzione non ha senso. Il fatto che il denominatore valga zero in un certo punto però non significa automaticamente che sia presente un asintoto, perché se anche il numeratore vale zero nello stesso punto (0/0) la funzione ha semplicemente un punto di discontinuità, ma senza asintoto.
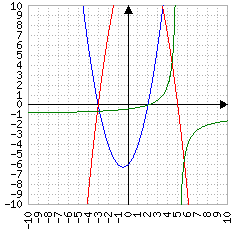
----------
-x^2+2x+15
In questo esempio, se x=-3 la funzione ha valore 0/0 e il comportamento della curva (in verde) apparentemente ignora questa particolarità.
In realtà, se si potesse ingrandire all'infinito il grafico (o se lo si rendesse "discreto") ci si accorgerebbe che la linea ha un "buco" in corrispondenza di x=-3 (infatti -3 non fa parte del dominio della funzione). Questo punto di discontinuità si chiama "del terzo tipo", ed è l'unico eliminabile facilmente.
Il più semplice esempio è x/x, che vale 1 per qualunque valore di x, tranne 0. In questo caso basta aggiungere un'"eccezione" alla funzione per trasformarla nuovamente in una funzione continua:
Se il numeratore ha un delta minore del denominatore, entrambi gli zeri sono interni agli asintoti, i limiti destri e i sinistri saranno diversi e si vedrà una figura con due "rami" esterni e una curva interna agli asintoti:
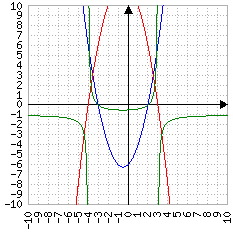
-----------
x^2-x+12
In questo esempio la distanza tra i due delta sinistri e i due delta destri è uguale, così la curva interna, che sta nell'intervallo ]-4, +3[, è perfettamente simmetrica, ma con valori diversi potrebbe essere anche distorta.
Se i due delta si "accavallano", per esempio il numeratore vale zero nei punti -1, 4 e il denominatore nei punti 0 e 7, i due "rami" esterni tenderanno a due infiniti diversi e quella che era una curva priva di flessi tra i due asintoti diventa una curva con un flesso. In ogni caso, in corrispondenza degli asintoti i limiti destro e sinistro sono diversi:
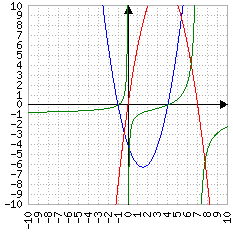
----------
-x^2+7*x
Si può fare un'ulteriore considerazione su questo tipo di funzione: se uno degli zeri cade in mezzo tra i due asintoti, e il delta del numeratore è > 0, per forza la parte a sinistra dello zero avrà segno diverso della parte destra.
Infine, se i due delta non si "intersecano", uno dei due "rami" conterrà i due zeri:
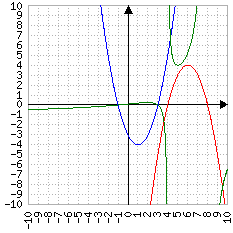
----------
-x^2+12*x-32