Algoritmo per scovare cicli in un grafo (passo passo)

Posted by On Filed under Algoritmi e strutture dati

Tratto dall'esame del 27/05/2017 di Algoritmi e Strutture Dati (M. Pelillo)

MyAlgorithm( A )
1. n = rows(A) /* determina il numero di vertici del grafo */
2. let B an n x n matrix /* alloca memoria per una matrice B n x n */
3. for i = 1 to n
4.   for j = 1 to n
5.     b[i,j] = 0
6.     for k = 1 to n
7.       b[i,j] = b[i,j] + a[i,k]*a[k,j]
8. for i = 1 to n
10.  for j = i + 1 to n
11.     if a[i,j]*b[i,j] <> 0 then
12.return FALSE
13.return TRUE

Evidentemente l'algoritmo è composto da due parti: nella prima si crea una matriche di dimensioni uguali alla matrice di adiacenza e si fa un calcolo.
Nella seconda, si verifia la matrice ottenuta in modo che se lo stesso elemento nella matrice di adiacenza e nella matrice calcolata contiene 1 si restituisca FALSE.

Esempio


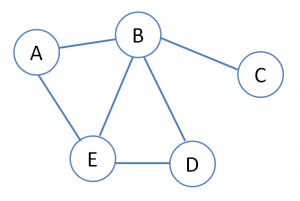
La matrice di adiacenza corrispondente è la seguente:

A B C D E
A - 1 0 0 1
B 1 - 1 1 1
C 0 1 - 0 0
D 0 1 0 - 1
E 1 1 0 1 -
  • i = 1
  • j = 1
  • k = 1 ⇒ 5

Matrice a

Matrice a
A B C D E
A - 1 0 0 1
B 1 - 1 1 1
C 0 1 - 0 0
D 0 1 0 - 1
E 1 1 0 1 -
Matrice b, k = 1
A B C D E
A 0
B
C
D
E
Matrice b, k = 2
A B C D E
A 1
B
C
D
E
Matrice b, k = 3
A B C D E
A 1
B
C
D
E
Matrice b, k = 4
A B C D E
A 1
B
C
D
E
Matrice b, k = 5
A B C D E
A 2
B
C
D
E

In effetti, quanti vertici collegati ha A in comune con A stesso? Due, cioè B ed E. Procediamo.

  • i = 1
  • j = 2
  • k = 1 ⇒ 5

Matrice a

Matrice a
A B C D E
A - 1 0 0 1
B 1 - 1 1 1
C 0 1 - 0 0
D 0 1 0 - 1
E 1 1 0 1 -
Matrice b, k = 1
A B C D E
A 2 0
B
C
D
E
Matrice b, k = 2
A B C D E
A 2 0
B
C
D
E
Matrice b, k = 3
A B C D E
A 2 0
B
C
D
E
Matrice b, k = 4
A B C D E
A 2 0
B
C
D
E
Matrice b, k = 5
A B C D E
A 2 1
B
C
D
E

In effetti, quanti vertici collegati ha A in comune con A stesso? Due, cioè B ed E. Procediamo.

  • i = 1
  • j = 3
  • k = 1 ⇒ 5

Matrice a

Matrice a
A B C D E
A - 1 0 0 1
B 1 - 1 1 1
C 0 1 - 0 0
D 0 1 0 - 1
E 1 1 0 1 -
Matrice b, k = 1
A B C D E
A 2 1 0
B
C
D
E
Matrice b, k = 2
A B C D E
A 2 1 1
B
C
D
E
Matrice b, k = 3
A B C D E
A 2 1 1
B
C
D
E
Matrice b, k = 4
A B C D E
A 2 1 1
B
C
D
E
Matrice b, k = 5
A B C D E
A 2 1 1
B
C
D
E

In effetti, quanti vertici collegati ha A in comune con A stesso? Due, cioè B ed E. Procediamo.

  • i = 1
  • j = 4
  • k = 1 ⇒ 5

Matrice a

Matrice a
A B C D E
A - 1 0 0 1
B 1 - 1 1 1
C 0 1 - 0 0
D 0 1 0 - 1
E 1 1 0 1 -
Matrice b, k = 1
A B C D E
A 2 1 1 0
B
C
D
E
Matrice b, k = 2
A B C D E
A 2 1 1 1
B
C
D
E
Matrice b, k = 3
A B C D E
A 2 1 1 1
B
C
D
E
Matrice b, k = 4
A B C D E
A 2 1 1 1
B
C
D
E
Matrice b, k = 5
A B C D E
A 2 1 1 2
B
C
D
E

In effetti, quanti vertici collegati ha A in comune con A stesso? Due, cioè B ed E. Procediamo.

  • i = 1
  • j = 5
  • k = 1 ⇒ 5

Matrice a

 

Matrice a
A B C D E
A - 1 0 0 1
B 1 - 1 1 1
C 0 1 - 0 0
D 0 1 0 - 1
E 1 1 0 1 -
Matrice b, k = 1
A B C D E
A 2 1 1 2 0
B
C
D
E
Matrice b, k = 2
A B C D E
A 2 1 1 2 1
B
C
D
E
Matrice b, k = 3
A B C D E
A 2 1 1 2 1
B
C
D
E
Matrice b, k = 4
A B C D E
A 2 1 1 2 1
B
C
D
E
Matrice b, k = 5
A B C D E
A 2 1 1 2 1
B
C
D
E

Qui termina l'elaborazione della prima delle cinque righe, per tutte le colonne e per tutte le adiacenze.
Cosa ci dice questo primo risultato?

Ci dice che il vertice A ha in comune:

  • con se stesso i vertici B ed E, per un totale di due
  • con B il vertice E, per un totale di uno
  • con C il vertice B per un totale di uno
  • con D i vertici B ed E, per un totale di due
  • con E il vertice B, quindi uno

Al termine del ciclo annidato, la tabella b prende i seguenti valori:

Matrice b, risultato finale
A B C D E
A 2 1 1 2 1
B 1 4 0 1 2
C 1 0 1 1 1
D 2 1 1 2 1
E 1 2 1 1 3

Possiamo osservare che anche se la matrice b contiene 25 valori, la diagonale principale rappresenta il numero di archi collegati al vertice in oggetto (es. il vertice A ha due archi, quindi il valore è 2).

Inoltre, essendo un grafo non orientato, anche la b gode della simmetria, quindi il "calcolo" vero e proprio consiste solo in 10 "celle" (n * (n-1) / 2).

Matrice b, significato di diagonale e simmetria
A B C D E
A 2 1 1 2 1
B 1 4 0 1 2
C 1 0 1 1 1
D 2 1 1 2 1
E 1 2 1 1 3

Se ora sovrapponiamo a e b (moltiplicandone i valori tra loro), otteniamo una matrice contenente alcuni archi:

Matrice a * b
A B C D E
A - 1 0 0 1
B 1 - 0 1 2
C 0 0 - 0 0
D 0 1 0 - 1
E 1 2 0 1 -

Conclusioni

Questo algoritmo serve a individuare se in un grafo sono presenti cicli composti da tre vertici.