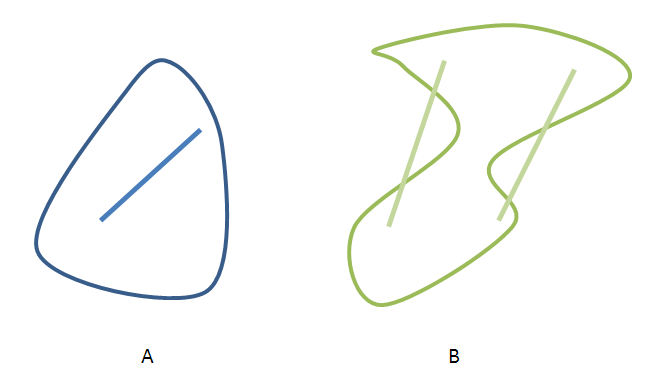
B è un insieme non convesso
Che un insieme sia convesso è determinato dal fatto che scelti due punti qualunque dell'insieme, tutti i punti della retta che li congiunge sono all'interno dell'insieme stesso.
Formalmente, dati due punti x e y appartenenti all'insieme, che chiameremo C, e un valore α compreso tra 0 e 1, vale la seguente:
αx+(1-α)y ∈ C
Table of Contents
Proposizione 5.1
Dati gli insiemi convessi C1...Cn, con n≥1, allora l'intersezione tra tutti gli insiemi
è un insieme convesso.
Dimostrazione
Se C è vuoto o contiene un solo elemento, la proposizione è immediatamente verificata.
Se contiene due elementi, per ciascuno degli insiemi C1...Cn vale che i due punti appartengono all'insieme.
È interessante osservare come il concetto di convessità si possa estendere anche a dimensioni superiori a 2, per esempio una sfera tridimensionale è convessa, e anche gli omologhi della sfera su più di tre dimensioni lo sono.
Definizione 5.2
...ovvero come capire se una funzione è concava o convessa.
Quando mi trovai di fronte per la prima volta a questo concetto, stavo studiando la derivata seconda di una funzione.
"In pratica - mi dicevo, per ricordare - se guido sopra la funzione e giro sempre a sinistra, la funzione è convessa, se giro a destra è concava. Se passo da sinistra a destra o viceversa, l'istante in cui il volante è dritto è il punto di flesso, dove la derivata seconda vale zero".
Un altro modo per capire se la funzione è convessa o concava, che concettualmente è più semplice della derivata seconda, è che se prendo due punti diversi tra loro della stessa funzione e li unisco con una linea retta, se la retta sta sopra la funzione, è convessa; se sta sotto è concava.
Formalmente, è convessa se:
f(αx+(1-α)y) ≤ αf(x)+(1-α)f(y), ∀α∈[0,1]
La parte a sinistra indica il valore della funzione in tutti i punti compresi tra x e y, la parte destra indica tutti i punti della retta che inizia in f(x) e termina in f(y).
Proposizione 5.3
Data la funzione f(x) con f:ℝn→ℝ, sia f(x) convessa su ℝn. L'insieme di livello (eventualmente vuoto) Lγ definito mediante la
Lγ = {x ∈ ℝn : f(x) ≤ γ}
è convesso per ogni γ ∈ ℝ
In altre parole, definito un insieme di livello come l'insieme di tutti i punti minori o uguali di f(x) (stiamo parlando di codominio di una funzione ℝn→ℝ, quindi di un insieme di punti appartenenti ai reali), se f(x) è convessa, anche Lγ lo sarà.