Studio di una funzione: log(x^2+5x-6)

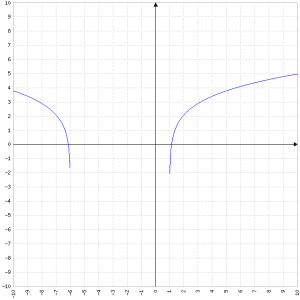
Funzione tratta da http://matepratica.tutorando.com

$ln (x^{2} + 5 x - 6)$

Table of Contents

Commento

La funzione è il logaritmo di una funzione di secondo grado, i cui zeri sono:

$\frac{- 5 \pm \sqrt{5^{2} + 24}}{2} = -6, 1$

Quindi x²+5x-6 si può scrivere anche (x+6)(x-1).

La funzione è maggiore di zero per gli intervalli esterni e minore di zero per quelli interni di -6, 1.

Dominio

x < -6 U x > 1, x∈ℝ

Zeri e segno

ln(x²+5x-6) = 0 ⇒ x²+5x-6 = 1

quindi x²+5x-7 = 0, che significa

$x = \frac{- 5 \pm \sqrt{53}}{2}$

I due zeri della funzione sono quindi:

$Z_{1} = \frac{- 5 + \sqrt{53}}{2}, 0$

$Z_{2} = \frac{- 5 - \sqrt{53}}{2}, 0$

La funzione è positiva da -∞ a Z₂, negativa da Z₂ a -6, ancora negativa da 1 a Z₁, e poi sempre positiva verso +∞.

Simmetrie

La funzione non è né pari né dispari.

Limiti

$\lim_{x \to \pm \infty} f (x) = + \infty$

Esistono asintoti verticali in corrispondenza dei limiti del dominio -6 e +1:

$\lim_{x \to {-6}^{-}} f (x) = \lim_{x \to 1^{+}} f (x) = - \infty$

Derivate

La derivata di una funzione composta g(f(x)) è g'(f(x)) * f'(x).

$\frac{2 x + 5}{x^{2} + 5 x - 6}$

Il denominatore è sempre positivo nel dominio; il numeratore 2x+5 > 0 ⇒ x > -5/2 è sempre negativo nella parte "sinistra" del dominio e sempre positivo nella parte "destra", come in effetti ci si poteva aspettare (parte "sinistra" sempre calante, parte "destra" sempre crescente).

La derivata seconda è:

	Num	Den
Prim	2x+5	x²+5x-6
Der	2	2x+5

$\frac{2 (x^{2} + 5 x - 6) - {(2 x + 5)}^{2}}{{(x^{2} + 5 x - 6)}^{2}} = \frac{- 2 x^{2} - 10 x - 37}{{(x^{2} + 5 x - 6)}^{2}}$

Dato che il numeratore della derivata seconda è negativo e ha delta negativo, la derivata ha sempre segno negativo; infatti la funzione non ha flessi e ha sempre un andamento di tipo ∩