Table of Contents
Dominio e codominio
Come regola, se non è esplicitamente richiesto che il dominio e il codominio di una funzione siano insiemi ℕ, ℤ o ℚ, il dominio su cui ci esercitiamo è quello dei numeri reali ℝ.
Le eccezioni più frequenti si riscontrano per prendere in considerazione tre casi particolari:
1) il dominio esclude lo zero, solitamente quando x sta al denominatore di una frazione.
f:ℝ→ℝ
f:x→1/x
non è valida, poiché con queste premesse x può essere = 0.
La formulazione corretta per la definizione del dominio è una delle seguenti:
f:ℝ*→ℝ
oppure
f:ℝ\{0}→ℝ
o in maniera più prolissa
f:{x|x∈ℝ, x≠0}→ℝ
2) il dominio considera solo i numeri positivi (e lo zero), solitamente quando x sta sotto radice pari.
√x è valida (siamo sempre nel dominio dei reali) solo se x > 0, quindi
f:ℝ→ℝ
f:x→√(x)
non è valida.
La formulazione corretta per la definizione del dominio è una delle seguenti:
f:ℝ+, {0}→ℝ
o in maniera più prolissa
f:{x|x∈ℝ, x≥0}→ℝ
3) il dominio considera solo i numeri positivi (e lo zero), solitamente quando x sta sotto radice pari.
f:ℝ→ℝ
f:x→log(x)
non è valida.
La formulazione corretta per la definizione del dominio è una delle seguenti:
f:ℝ+→ℝ
o in maniera più prolissa
f:{x|x∈ℝ, x>0}→ℝ
Equazioni e disequazioni di secondo grado
Le equazioni di secondo grado sono quelle espresse nella forma ax2+bx+c, ovviamente con a≠ 0, altrimenti saremmo di fronte a un'equazione di primo grado.
L'equazione è espressa anche come a0x0+a1x1+a2x2, ovvero a0+a1x+a2x2
Significato di a
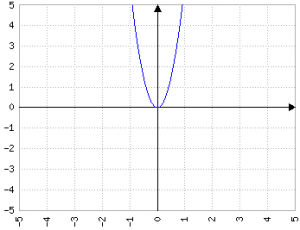
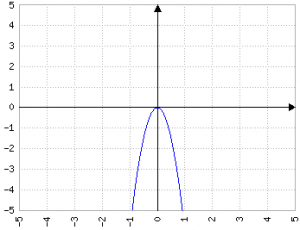
Il segno del primo termine è rappresentato dal "verso" della parabola corrispondente: per ax2 > 0 la parabola è rivolta "verso l'alto", mentre con ax2 < 0 la parabola è rivolta verso il basso (ricordo che con ax2 = 0 l'equazione è una retta, quindi il caso non è considerato qui).
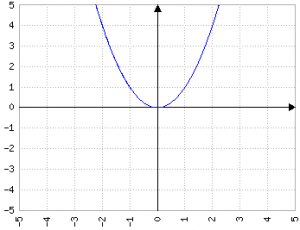
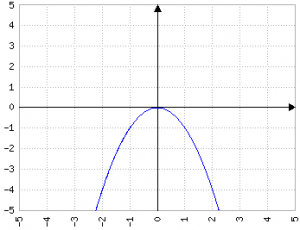
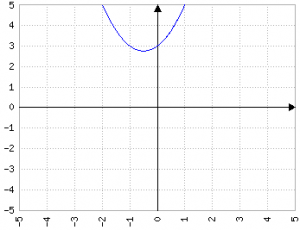
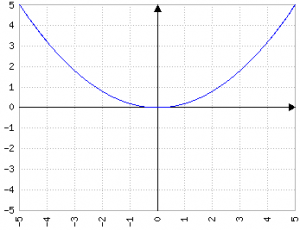
Il valore di a in ax2 indica quanto la parabola è "aperta", in maniera inversamente proporzionale: più a è grande, più la parabola è stretta:
Fig.3a: y=0.2x2; Fig.3b: y=-0.2x2
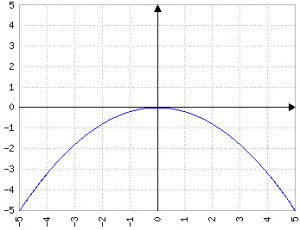
Finora tutte le parabole esaminate passano per il punto (0,0), poiché il primo elemento determina solo la "forma" e il "verso" della parabola, ma non lo spostamento sugli assi y e x.
Significato di b
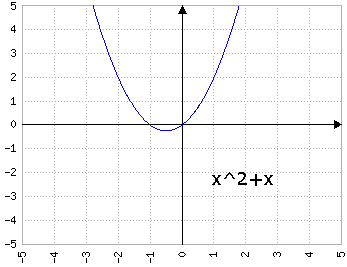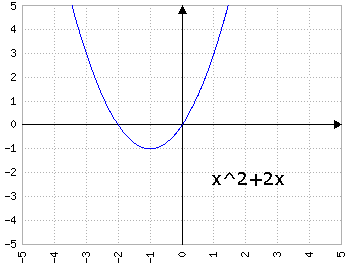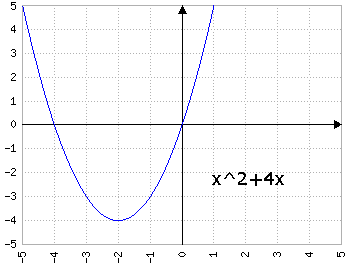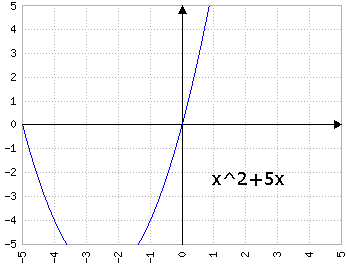
Il valore di b in ax^2+bx fa "scivolare" la parabola, facendola sempre passare per il punto (0,0).
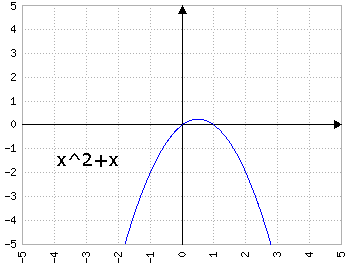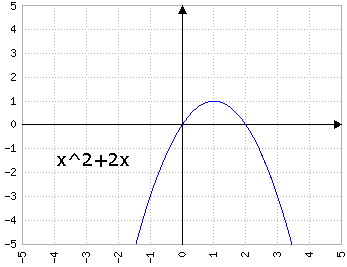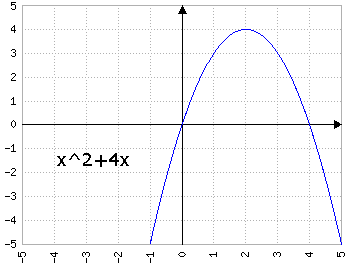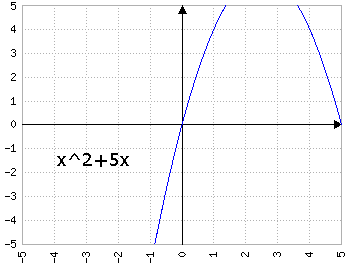
Fig.4a: y=x2+bx, dove b prende i valori di 1, 2, 3, 4, 5 - animazione
con a>0, b>0 fa "scivolare" la parabola "a sinistra", cioè il vertice si posiziona in (x, y) con x<0 e y<0.
Fig.4b: y=x2-bx, dove b prende i valori di -1, -2, -3, -4, -5 - animazione
con a>0, b<0 fa "scivolare" la parabola "a destra", cioè il vertice si posiziona in (x, y) con x>0 e y<0.
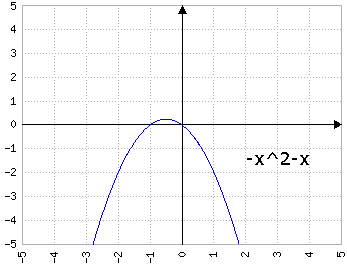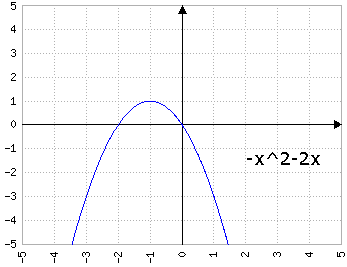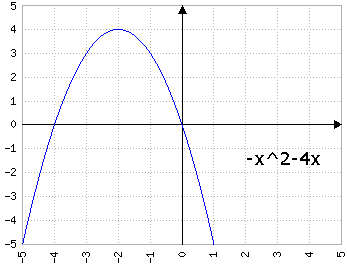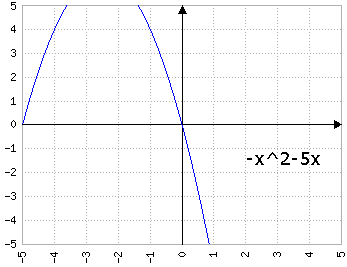
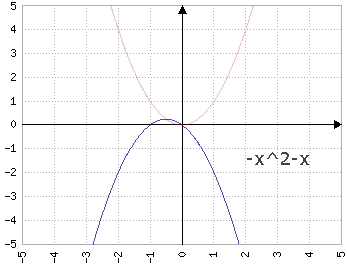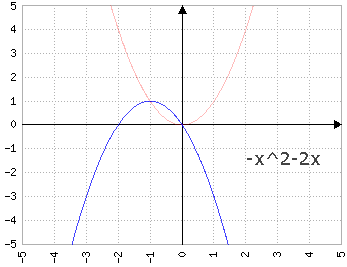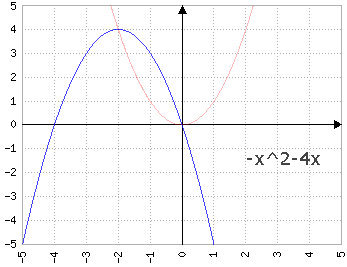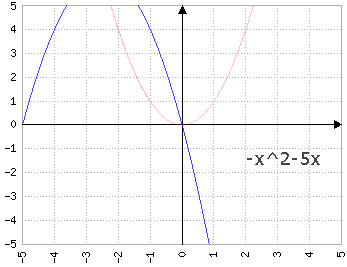
Fig.4c: y=-x2+bx, dove b prende i valori di 1, 2, 3, 4, 5 - animazione
con a<0 il comportamento di b si inverte, e b>0 fa "scivolare" la parabola a destra e b<0 a sinistra:
Fig.4d: y=x2-bx
NOTA: la parabola si sposta in diagonale in modo che un punto passi sempre per (0,0) (se c=0), e il vertice passi sempre per la parabola opposta:
Fig.5: y=-x2-bx confrontato con y=x2 (in rosso)
Significato di c
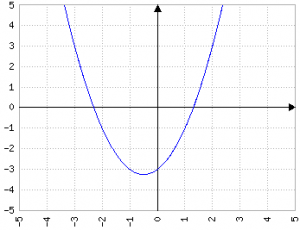
Il valore di c in ax2+bx+c indica quanto la parabola si sposta lungo l'asse x.
Fig.6a: y=x2+x-3
Significato di discriminante
Nella formula per trovare le soluzioni delle equazioni di secondo grado:
si chiama discriminante (Δ) la parte sotto radice quadrata b2-4ac.
Nell'àmbito dei numeri ℝ siccome Δ è sotto radice quadrata, il risultato di b2-4ac deve essere > 0, quindi se b2-4ac < 0 l'equazione non ha soluzioni.
Se il discriminante è = 0, è indifferente, nella formula riportata sopra, sommare o sottrarre la radice di zero, quindi l'equazione ha una sola soluzione, che corrisponde a
Si noti come il termine c scompaia dal risultato se la soluzione è unica.
Se il discriminante è > 0, le soluzioni sono due, una con +Δ e una con -Δ.
Calcolo delle soluzioni
Automatizzare il calcolo delle soluzioni è relativamente semplice, con un foglio di calcolo:
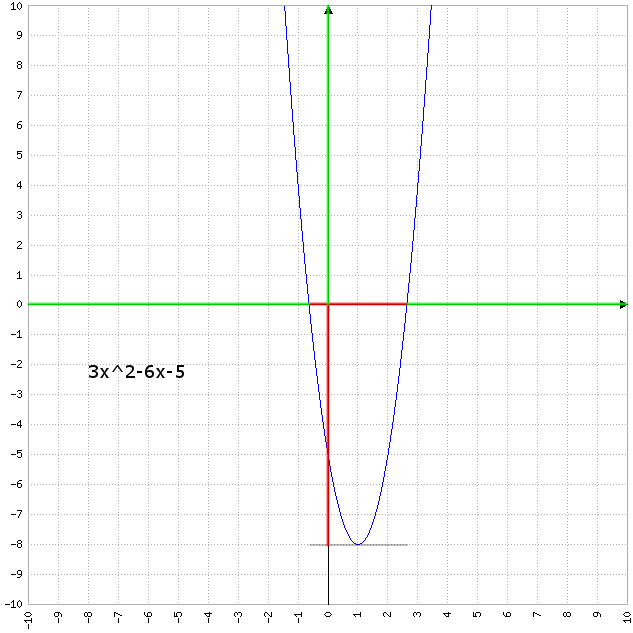
Disequazioni di secondo grado
Una disequazione di secondo grado ha valore per l'intervallo di x per cui y è positivo, se x > 0, oppure per cui y è negativo, se x < 0.
Se il segno dell'elemento di grado due è positivo, per x > 0 la disequazione ha come soluzione la parte "esterna" della parabola, per x < 0 ha come soluzione la parte "interna".
Se il segno dell'elemento di grado due è negativo, si inverte tutto, come si capisce facilmente dall'immagine: