Table of Contents
Dominio
Determino dove il denominatore è zero:
Dom: ℝ\{2, 4}
Dal momento che le radici del numeratore sono diverse da quelle del denominatore (vedi sotto: 3, 1), possiamo dire che in x=2 e x=4 sono presenti due asintoti verticali.
Intersezioni con gli assi
Determino dove il numeratore è zero:
Gli zeri sono in corrispondenza di x=1 e x=3:
P1 = (1, 0)
P2 = (3, 0)
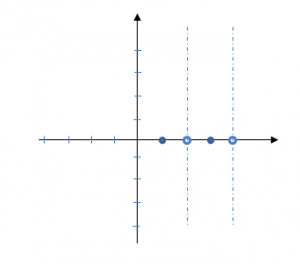
È facile verificare che l'intersezione con il punto y è a x=0 e y=3/8.
Parità
Una funzione di secondo grado con il fattore di primo grado diverso da zero è sempre né pari né dispari.
La divisione di due funzioni di secondo grado diverse tra loro non è né pari né dispari.
Segno
Il segno è determinato dal prodotto dei segni del numeratore e del denominatore.
Essendo entrambe funzioni con il primo termine > 0, sono positive per gli intervalli esterni agli zeri e negative per quelli interni:
1 2 3 4
x^2-4x+3 + | - | - | + | +
x^2-6x+8 + | + | - | - | +
------------+---+---+---+---
f(x) + | - | + | - | +
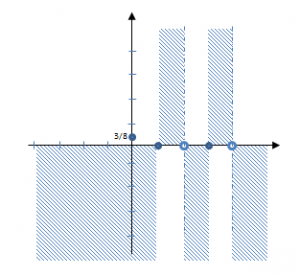
f(x) > 0 ⇒ x < 1 ⋃ 2 < x < 3 ⋃ x > 4
f(x) < 0 ⇒ 1 < x < 2 ⋃ 3 < x < 4
Limiti
I limiti da verificare sono:
- limite a ±∞
- limite destro e sinistro a +2 e +4
- limiti obliqui?
Di questo sviluppo, x^2 al numeratore si semplifica con quello al denominatore; le frazioni n/xm tendono a zero e si possono ignorare.
Resta un 1/1, che fa da limite sia a +∞ sia a -∞
Sia a +2 sia a +4 non esiste UN limite, ma una coppia di limiti, entrambi a ±∞

Minimi e massimi
Calcolo della derivata di una frazione.
Formula generale per il calcolo della derivata di una espressione razionale (f(x) è il numeratore, g(x) il denominatore):
Sviluppo il numeratore, lascio così com'è il denominatore:
Siccome il denominatore è sempre positivo (è il quadrato di qualcosa, quindi è SEMPRE positivo o zero), detta il segno il numeratore.
Il Δ del numeratore è:
Con un Δ < 0 non esistono né minimi locali né massimi locali.
In parole poco precise ma molto descrittive, la funzione "scende" sempre.
Punti di flesso
Per derivare un polinomio al quadrato il risultato è f'(x) f(x)
quindi: ((x^2-6x+8)^2 )' = 2(2x-6)(x^2-6x+8)
La derivata del numeratore invece è -4x+10
Facciamo due conti: