7. Limiti e asintoti

La lezione 7 ha riguardato:

1. Esempi di limiti
2. Asintoti
3. Teoremi sulle funzioni continue

Esempi di limiti

Dimostrazione che (1+t)ⁿ≥1+nt (disuguaglianza di Bernoulli)

Con t∈ℝ e t>-1, ∀ n∈ℕ

${\left(1+t\right)}^n\ge 1+nt$

Dim. per induzione (1) base: per n=1, (1+t)¹ = 1+t ≥ 1+(1·t) = 1+t (2) passo induttivo: Supponiamo per n>1

${\left(1+t\right)}^n\ge 1+nt$

Sviluppiamo calcolando il passo n+1, moltiplicando entrambi i membri per 1+t

${\left(1+t\right)}^{\mathrm{n+1}}\ge \left(1+nt\right)·\left(1+t\right)$ ${\left(1+t\right)}^{\mathrm{n+1}}\ge 1+t+nt+n{t}^2$

Raccogliamo t:

${\left(1+t\right)}^{\mathrm{n+1}}\ge 1+\left(1+n\right)·t+\sout{n{t}^2}$

Dal momento che nt² è sicuramente > 0 per definizione, togliere questo termine non indebolisce la disuguaglianza:

${\left(1+t\right)}^{\mathrm{n+1}}\ge 1+\left(1+n\right)·t$

che è l'ipotesi del passo induttivo. Q.E.D.

Limite per qⁿ con 0≤q≤1

con q,n∈ℝ, trovare il limite:

$\underset{n\to \mathrm{+\infty }}{\lim }{a}_n=q^n$

Poniamo

$q=\frac{1}{1+t}$

e "giriamo" l'equivalenza così:

$t=\frac{1}{q}-1$

abbiamo che

$0<q^n={\left(\frac{1}{1+t}\right)}^n$

per la disuguaglianza di Bernoulli (vedere sopra) abbiamo

${\left(\frac{1}{1+t}\right)}^n\le \frac{1}{1+nt}\le \frac{1}{nt}$

Ora, il limite di zero (costante) è zero:

$\underset{n\to \mathrm{+\infty }}{\lim }{a}_n=q^n\ge \underset{n\to \mathrm{+\infty }}{\lim }0$

Inoltre è minore o uguale al limite 1/nt:

$\underset{n\to \mathrm{+\infty }}{\lim }{a}_n=q^n\le \underset{n\to \mathrm{+\infty }}{\lim }\frac{1}{nt}=0$

per il teorema di compressione

$\underset{n\to \mathrm{+\infty }}{\lim }{a}_n=0$

Se q = -1 il limite non esiste, perché i valori sono -1⁰ = 1, -1¹ = -1, -1² = 1, -1³ = -1, 1, -1, 1, -1... Invece con |q| > 1, ponendo q=1+t vale

$q^n\ge {\left(1+t\right)}^n\ge 1+nt$

e siccome

$\underset{n\to \infty }{\lim }1+nt=\infty$

anche il limite di qⁿ tende a +∞ (per n pari) o -∞ (per n dispari) Riassumendo:

$\underset{n\to \infty }{\lim }{q}^n=\left\{\begin{array}{cc}0& \text{se q∈(-1,1)}\\ 1& \text{se q=1}\\ \mathrm{+\infty }& \text{se q>1}\\ \text{non esiste}& \text{se q≤0}\end{array}\right.\text{inoltre}\underset{n\to \mathrm{-\infty }}{\lim }{q}^n=\left\{\begin{array}{cc}\mathrm{+\infty }& \text{se q∈(-1,1)}\\ 1& \text{se q=1}\\ 0& \text{se q>1}\\ \text{non esiste}& \text{se q≤0}\end{array}\right.$

Asintoti

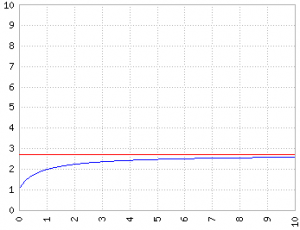
Gli asintoti sono rette a cui una funzione tende (senza mai raggiungere). Gli asintoti possono essere orizzontali (costante), verticali o diagonali.

Un esempio di asintoto orizzontale è e per la funzione (1+1/n)ⁿ

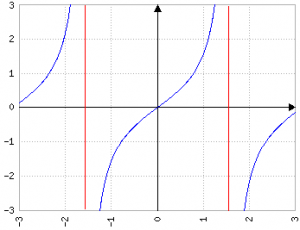
Un esempio di asintoto verticale è il valore di tg(x) in π/2 (o ancora meglio kπ+π/2)

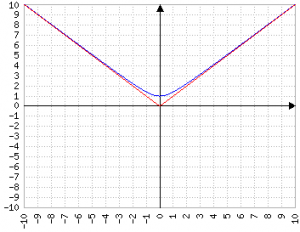
Un esempio di asintoto diagonale è sqrt(1+x^2):

Teoremi sulle funzioni continue

Valori intermedi

• sia f:[a,b]→ℝ continua in [a,b]
• sia y∈ℝ compreso tra f(a) e f(b)

∃ x∈[a,b] t.c. f(x)=y

in altre parole, meno rigorose ma più chiare, se f(x) è continua in un intervallo, lo è anche la sua immagine.

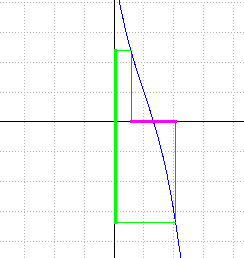
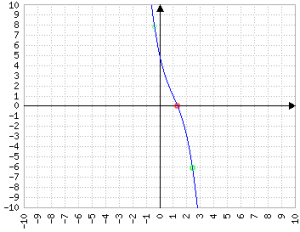
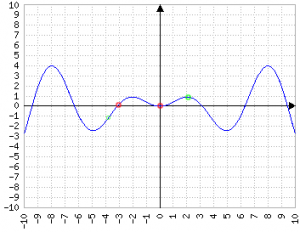
Bolzano, o dei due zeri

• sia f:[a,b]→ℝ continua in [a,b]
• sia f(a)·f(b) < 0 ⇒ sgn(f(a)) ≠ sgn(f(b))

∃ almeno un x∈[a,b] t.c. f(x)=0

 

---

Weierstrass

• sia f:[a,b]→ℝ continua in [a,b]
• se ∃ k∈ℝ, k>0 t.c. |f(x)|<k ∀ x∈[a,b]

∃ x₀, x₁ t.c. f(x₀)≤f(x)≤f(x₁) ∀ x∈[a,b]

x₀ è minimo assoluto
x₁ è massimo assoluto