4. funzioni elementari

La lezione 4 ha riguardato:

1. Funzioni inverse
2. Funzioni polinomiali (cenni)
3. Funzioni razionali (cenni)
4. Potenze (cenni)
5. Cenni di limiti (cenni)
6. Logaritmi (cenni)
7. Funzioni trigonometriche (cenni)

Funzioni inverse

Data una funzione f:A→B posso costruire una f ^-1:f(A)→A dove f(A)⊆B tale che f^-1∘f(a) = a ∀ a∈A e f∘f^-1(b) = b ∀ b∈f(A).

Perché una funzione possa avere una funzione inversa, deve essere INIETTIVA.

Esempio

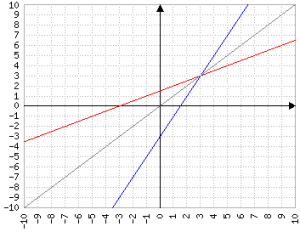
La funzione f:ℝ→ℝ che manda x→2x-3 è iniettiva (è infatti una funzione che rappresenta una retta nella forma ma+b con m≠0) e quindi ha una funzione inversa, che è (x+3)/2.

Il grafico delle due funzioni è speculare lungo la retta y=x:

Funzioni polinomiali

La funzione f:ℝ→ℝ si dice polinomiale se f(x) = 0 + a₁x + a₂x² + a₃x³... + a_nxⁿ

con a≠0, a∈ℝ, n∈ℕ

Si dice grado l'esponente più grande.

Zeri delle funzioni polinomiali

Per i polinomi di grado 1 lo zero è la parte costante (la "b" di ax+b).

Nei polinomi di grado 3 e 4 gli zeri sono calcolabili solo utilizzando i numeri complessi ℂ.

Nei polinomi di grado 2 la formula è

Siccome la formula ha come codominio i reali, a seconda del valore di b²-4ac gli zeri possono essere:

• 2: il risultato è > 0, quindi si hanno una soluzione per +(b²-4ac) e una per -(b²-4ac)
• 1: il risultato è = 0, quindi si mantiene la sola parte -b/2c
• 0: il risultato è < 0, quindi non è possibile trovare soluzioni con radice di un numero negativo

Inoltre valutando a si può capire il "verso" della parabola:

• a > 0: la parabola è "rivolta" verso l'alto
• a = 0: la parabola perde il suo elemento di grado 2, quindi diventa una retta
• a < 0: la parabola è "rivolta" verso il basso

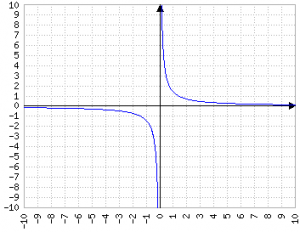
Funzioni razionali

Si dice funzione razionale una funzione f:ℝ→ℝ\{q(x)=0} con x∈ℝ nella forma p(x)/q(x).

Esempio

f(x):ℝ→ℝ
f(x):x→7/5x

Potenze

Potenze con esponente n naturale

Dati a∈ℝ, n∈ℕ
aⁿ = a*a*a*a*...a n volte

Potenze con esponente 1/n e n naturale

Dati a∈ℝ⁺, n∈ℕ

a^1/n = ⁿ√a

Potenze con esponente m/n e m,n naturali

Dati a∈ℝ⁺ se m pari, a∈ℝ se m dispari, m,n∈ℕ, n≠0

a^m/n = ⁿ√a^m

Potenze con esponente reale approssimato tramite limite

Dati a∈ℝ, n∈ℝ
aⁿ = r con r∈ℝ, ∃ una successione di razionali il cui limite è r.

Data la successione a₁, a₂, a₃, ... a_m, dato un ε > 0, ∃ m∈ℕ > 0 tale che |a_t-r| < ε ∀ t∈ℕ, t > m

Logaritmi

Data una funzione f:ℝ⁺→ℝ⁺
f:x→x²

La funzione inversa f ^-1:ℝ⁺→ℝ⁺
f:y→log_ay

a^x=y, log_ay=x

Funzioni trigonometriche

sen(α) è f:ℝ→{x|x∈ℝ, -1≤x≤1}
Dove α è un angolo espresso in radianti (multipli di π).

Il seno è la proiezione sull'asse delle ordinate (il coseno su quello delle ascisse) del raggio di un cerchio (con raggio = 1) con angolo α che parte dalla zona positiva dell'asse x.