Novembre 2016 Archive

Esercizi per il corso di Probabilità e Statistica

Foglio 1: Statistica descrittiva

Esercizio 1

Per ognuna delle seguenti variabili si dica se si tratta di una variabile quantitativa (discreta o continua) o qualitativa (nominale o ordinale):

1. l'età degli studenti in questo corso;
2. i programmi preferiti dalle studentesse di questo corso;
3. il numero degli studenti di questo corso che guardano la trasmissione "X Factor";
4. le spese di trasporto sostenute dagli studenti di questo corso;
5. il voto riportato all'esame di matematica;
6. l'aver superato l'esame di matematica.

Risposte

1. continua
2. nominale
3. discreta
4. discreta
5. discreta

Esercizio 2

Il docente di un corso universitario ha raccolto alcuni dati sugli studenti che hanno sostenuto il suo esame. La tabella riporta i dati relativi ai primi quattro studenti.

Voto	Anno di corso	Residenza	Diploma Sup. Frequentante
28	I	Treviso	Liceo S
21	IV	Venezia	Ist. Tecnico N
18	I	Verona	Ist. Comm. S
21	II	Padova	Ist. Prof. S

1. Qual è l'unità statistica? Qual è la popolazione di riferimento?
2. Quali caratteri (variabili) sono rilevati?
3. Quali sono le modalità rilevate del Diploma Superiore?
4. Quali sono le modalità rilevate del Voto e quali quelle possibili?

Risposte

1. L'unità statistica è lo studente e la popolazione è l'insieme degli studenti che hanno superato l'esame.
2. Sono rilevati il voto, l'anno di corso, la residenza e il diploma di scuola superiore
3. Le modalità rilevate del diploma superiore sono: Liceo S, Ist. Tecnico N, Ist. Comm. S, Ist. Prof. S...
4. Le modalità rilevate del voto sono ins, 18, 19, 20,... 30, 30L (non è specificato che l'esame sia superato)

Esercizio 3

In un gruppo di 20 persone sono state rilevate due variabili, il sesso e l'età

47 61 38 40 26 41 49 65 53 55
F  M  M  M  F  M  F  F  M  F
30 23 34 33 40 21 65 32 47 50
M  F  M  F  M  M  M  F  F  F

1. Si costruisca la distribuzione per classi dell'età (utilizzando le classi 19-29, 30-44, 45-59, 60 e oltre) e si calcolino le frequenze assolute, relative, percentuali, le cumulate e le densità di frequenza. Si disegni un opportuno istogramma.
2. Si rappresenti la funzione di ripartizione empirica e se ne calcoli il valore nel
   punto 57.
3. Si disegni il diagramma a scatola con baffi, partendo dai dati originari.
4. Si calcolino media, varianza, scarto quadratico medio, campo di variazione,
   scarto interquantile e coefficiente di variazione.
5. Si chiamino yi i valori originari e zi quelli standardizzati: si trovino media e
   varianza degli zi attraverso le corrispondenti quantità degli yi.

Risposte

1. 	freq. ass	f. rel.	%	ass. cum	rel. cum	dens.
   19-29	3	0,15	15	3	0,15	0,3
   30-44	8	0,4	40	11	0,55	˜0,57
   45-59	6	0,3	30	17	0,85	˜0,43
   60+	3	0,15	15	20	1	0,6

   Grafico:

   

2. Grafico della ripartizione empirica:
   
   Ripartizione empirica = frequenza relativa di unità con valore ≤ x.
   La ripartizione empirica di 57 è 0,85.
3. Grafico:
   
   
4. Dati A = l'insieme dei valori; n = il numero di elementi in A; A(i) l'i-esimo elemento di A (i ∈ ℕ):
   • media
     $\frac{\sum _{i=1}^{n}A\left(i\right)}{n}$Usando R, si ottiene che mean(A) = 42,5
   • varianza
     $\frac{\sum _{i=1}^n{\left(A\left(i\right)-media\left(A\right)\right)}^2}{n}$La media dei quadrati è 1973,2, il quadrato della media è 1806,25, quindi la varianza è 166,95
   • scarto quadratico medio (radice della varianza): ˜12,92
   • campo di variazione: la differenza tra il valore più alto (65) e il più basso (21): 65-21 = 44
   • scarto interquantile: differenza tra il terzo e il primo quartile. [21 23 26 30 32] [33 34 38 40 40] [41 47 47 49 50] [53 55 61 65 65] 50-32 = 18
   • coefficiente di variazione ⇒?

Esercizio 4

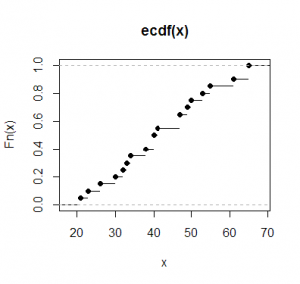
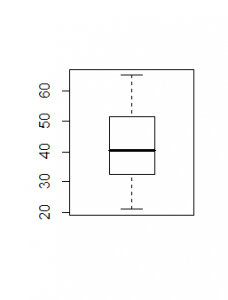
L'assistenza tecnica di un rivenditore di computer ha registrato le richieste di intervento in un particolare giorno. Il risultato è stato:

H,H,M,S,H,M,M,S,H,S,S,M,H,M,M,S,M

dove H=problemi hardware, S=problemi software, M=guasto monitor.

1. Calcolare la distribuzione delle frequenze assolute e relative; disegnare il diagramma a barre;
2. calcolare un indice di posizione opportuno

Risposte

1. 	F. ass.	F. rel
   H	5	˜0,29
   S	5	˜0,29
   M	7	˜0,41

2. L'indice di posizione opportuno è la moda, il cui valore è M (guasto al monitor)

Esercizio 5

Nella tabella sottostante sono riportati i consumi (in milioni di tonnellate) di risorse naturali impiegate nell'economia italiana nel quinquennio 2000-2004 e le importazioni delle medesime risorse nello stesso arco temporale.

             2000     2001     2002       2003     2004
Fabbisogno      2.357    2.295    2.214      2.077    2.184
Importazioni  329.028  330.035    334.807  343.784  360.282

1. Si rappresentino graficamente i dati;
2. si calcolino la covarianza e il coefficiente di correlazione e si dia un'interpretazione dei risultati.

Esercizio 6

Il responsabile della sicurezza di una grossa azienda ha rilevato il numero di tentativi di intrusione bloccati ogni giorno durante i primi 14 giorni del mese:

56 47 49 37 38 60 50 43 43 59 50 56 54 58

Dopo aver cambiato le impostazioni del firewall, le intrusioni bloccate nei 20 giorni
successivi sono state

53 21 32 49 45 38 44 33 32 43 53 46 36 48 39 35 37 36 39 45

Al fine di valutare l'efficacia delle nuove impostazioni, si confrontino il numero di tentativi di intrusione bloccati prima e dopo il cambio, calcolando il summary dei dati, tracciando i boxplot appaiati e commentando i risultati ottenuti.

Esercizio 7

I dati seguenti rappresentano il numero di registrazioni di nuovi account in dieci giorni consecutivi ad un sito di vendite online:

43 37 50 51 58 105 52 45 45 10

1. Calcolare media, mediana, quartili e deviazione standard.
2. Trovare gli outlier (osservazioni anomale) usando la regola 1:5Xdistanza interquartile.
3. Eliminare gli outlier trovati e calcolare nuovamente media, mediana, quartili e scarto quadratico medio.
4. Trarre delle conclusioni sull'influenza degli outlier sugli indici calcolati.

Esercizio 8

Un provider vuole valutare il carico della sua rete e registra il numero di utenti (in migliaia di persone) connessi contemporaneamente in 50 luoghi:

17.2 22.1 18.5 17.2 18.6 14.8 21.7 15.8 16.3 22.8
24.1 13.3 16.2 17.5 19.0 23.9 14.8 22.2 21.7 20.7
13.5 15.8 13.1 16.1 21.9 23.9 19.3 12.0 19.9 19.4
15.4 16.7 19.5 16.2 16.9 17.1 20.2 13.4 19.8 17.7
19.7 18.7 17.6 15.9 15.2 17.1 15.0 18.8 21.6 11.9

1. Calcolare la media campionaria, la varianza e lo scarto quadratico medio dei dati rilevati.
2. Calcolare il summary e costruire il boxplot.
3. Calcolare lo scarto interquantile. Sono presenti delgli outliers?
4. Tracciare un istogramma e commentare la simmetria della distribuzione.

Ω

Ω rappresenta l'insieme dei possibili risultati. La probabilità di tutti gli eventi che appartengono a Ω è 1.

ω

ω rappresenta un elemento dell'insieme Ω, cioè l'esito di un singolo evento.

$\stackrel{\mathrm{----}}{\Omega }$

$\stackrel{\mathrm{----}}{\Omega }$ è l'insieme complementare di Ω, cioè un evento impossibile. Qualunque insieme con una "barretta" sopra è l'insieme degli esiti diversi dall'insieme rappresentato. Si può rappresentare anche con 1 - P(A), cioè 1 meno la probabilità che si verifichi un evento di A

P(A)

P(A), con A ⊆ Ω è la probabilità che si verifichi uno degli eventi dell'insieme A.

P(A_i) è la probabilità che si verifichi l'i-esimo elemento dell'insieme A. A volte, senza tirare in ballo l'insieme A, si indica con p_i